Необходимые знания

4.2.1. Общие сведения о пересечении тел.

При решении этой задачи, прежде всего, необходимо определить характер линии пересечения, которая зависит от вида пересекающихся поверхностей и их взаимного расположения.

В РГР №3 рассматриваются три основных случая пересекающихся поверхностей:

- пересечение многогранников;

-пересечение многогранника с поверхностью второго рода;

- пересечение поверхностей второго рода.

В каждом из этих случаев для определения линии пересечения поверхностей применяются свои способы и приемы ее построения, но суть их общая и сводится к следующему (рис. 13).Обе заданные поверхности пересекают вспомогательной поверхностью или плоскостью - посредником а. Затем находят линии пересечения b* иb каждой из поверхностей с посредником а. Точки пересечения этих линий М и N принадлежат кривой пересечения поверхностей. Изменяя положение посредника набирают необходимое количество точек М и N, по которым строится кривая пересечения тел.

Рис. 13. Определение линии пересечения поверхностей

В качестве посредников выбирают удобно расположенные плоскости (общего положения, проецирующие плоскости, плоскости уровней) или поверхности (сферические, цилиндрические, конические и т.д.).

4.2.2. Пересечение многогранников.

В этом случае линией пересечения будет замкнутая пространственная ломаная, состоящая из отрезков прямых, по которым пересекаются плоскости граней. Точки излома будут принадлежать ребрам многогранников.

Рассмотрим построение линии пересечения на примере шестигранной пирамиды SKLMNPR с трехгранной призмой ABCDEF (рис 14).

Для ее построения необходимо выделить ребра и грани, участвующие в пересечении. Здесь это ребра пирамиды (SK, SL, SM, SN, SP, SR) и грани призмы (ABFE, EFCD). Кроме того, следует отметить, что ребра SK и SNпирамиды пересекаются только с ребром EF призмы.

Определение положения точек излома сводится к определению положения точек встречи прямых с плоскостями (точки 1,2, 4 и 5) и точек пересечения пересекающихся прямых (точки 3 и 6). В первом случае за плоскости принимают грани призмы, а за прямые - ребра пирамиды, через которые проводится вспомогательная проектирующая плоскость - посредник а. Во втором случае за прямые принимают пересекающиеся ребра многогранников.

Рис. 14. Построение линии пересечения многогранников

При определении положения точек излома целесообразно выбирать направление их обхода по часовой или против часовой стрелки (в примере по часовой стрелке), что позволяет избежать ошибок в построениях.

Видимость линии пересечения определяется при помощи, конкурирующих точек.

4.2.3. Пересечение многогранника с поверхностью второго рода.

В этом случае линией пересечения будет пространственная ломаная, состоящая из дуг кривых, по которым поверхность второго рода пересекается с плоскостями граней. Точки излома будут принадлежать ребрам многогранника.

Рассмотрим порядок построения линии пересечения на примере пересечения конуса с трехгранной призмой (рис. 15).

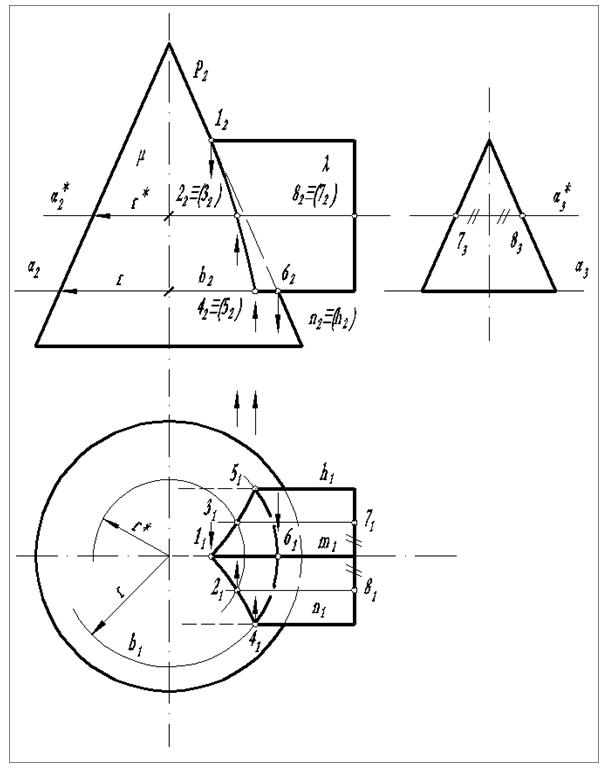
Рис. 15. Пример пересечения конуса с трехгранной призмой

Решение данной задачи заключается в нахождении точек встречи ребер многогранниках поверхностью конуса.

Для этого в качестве плоскости-посредника целесообразно исполь­зовать плоскость уровня а.

Определение точек излома. Здесь следует отметить, что точку встречи ребра т с поверхностью конуса можно определить как общую точку двух пересекающихся прямых, т.е. ребра т и образующей р(m₂∩p₂)=l₂→l₁, l₃. Для получения других точек излома воспользуемся плоскостью - посредником α, которую проведем через грань, образованную ребрами k и п. Линией сечения конуса будет окружность радиуса r. Точки пересечения 4 и 5 этой окружности и ребер k и п являются точками излома линии пересечения поверхностей λ иμ т.е. k₁∩b₁=5₁→5₂ и n₁∩b₁=4₂→4₂.

Определение точек дуг. Здесь следует обратить внимание на то, что дуга между 4 и 5 точками излома на плоскости проекций совпадет с линией сечения конуса с плоскостью-посредником а, т.к. плоскость а≡(k∩n). Положения промежуточных точек для других дуг, например 2 и 3, определяются как точки пересечения линий сечений поверхностей плоскостью-посредником а^*.

После определения необходимого количества точек наносят линию пересечения поверхностей с учетом ее видимости. Для нанесения дуг целесообразно использовать лекало. Видимость линии пересечения определяется с помощью конкурирующих точек.

4.2.4. Пересечение двух поверхностей второго порядка.

В случае пересечения двух кривых поверхностей второго порядка образуется пространственная кривая четвертого порядка.

Для построения линии пересечения поверхностей следует найти достаточное количество точек, в том числе характерных - высшую и низшую - на очерковых образующих. Определение положения точек может быть достигнуто двумя способами: способом вспомогательных плоскостей и способом вспомогательных сфер. Первый способ применяют, если вспомогательные плоскости пересекают поверхности по графически простым линиям, например окружностям. Применение этого способа характерно для тел, оси вращения которых параллельны или пересекаются (скрещиваются) под прямым углом. Второй способ применяют, когда оси вращения тел пересекаются не под прямым углом не равным.

Способ вспомогательных плоскостей (рис.16). В качестве плоскости- посредника целесообразно использовать плоскость уровня α, т.к. она рас­секает обе поверхности по окружности.

Определения точек линии пересечения поверхностей аналогична методике приведенной выше (см. пересечение многогранника с поверхностью второго рода).

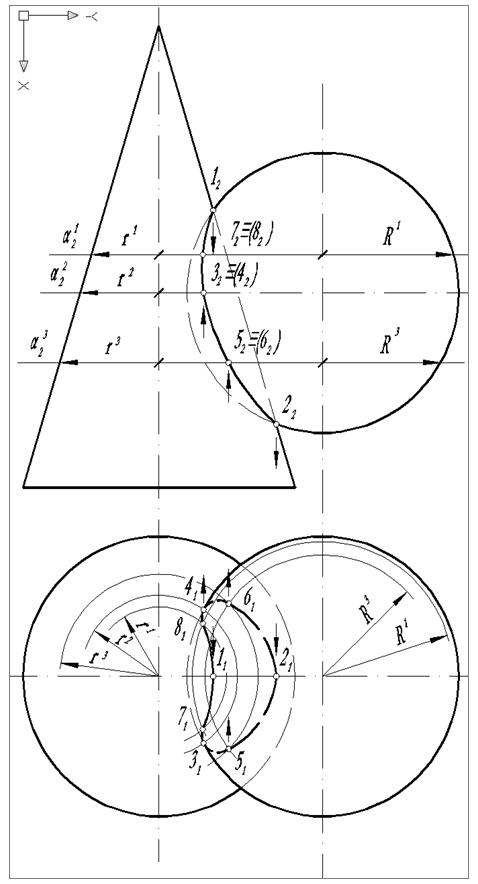
Рис. 16. Пример пересечения конуса и сферы

Сама линия пересечения строится:

- на фронтальной проекции видна ближняя часть кривой (1₂-4₂-6₂-2₂) и не видна дальняя (1₂-3₂-5₂-2₂);

- кривая пересечения поверхностей на фронтальной проекции симметрична, значит (1₂-4₂-6₂-2₂) ≡(1₂-3₂-5₂ -2₂);

-на горизонтальной проекции видна часть кривой (3₁-1₁ -4₁), расположенная выше экватора сферы, границей видимости служат точки на экваторе 3₁ и 4₁.

Способ вспомогательных сфер (рис. 17). Применяется для построения линии поверхностей тел вращения, имеющих пересекающиеся оси. Этот способ применим, когда оси сфер пересекаются, и плоскость, образованная осями, является плоскостью уровня.

Выберем центр вспомогательных сфер в точке пересечения осей заданных поверхностей (точка О).

Точки 1 и 2 на очерковых образующих, расположенные в одной плоскости, определяются непосредственно. Линия пересечения заключается между этими точками. Одна из них определяет максимальный радиус вспомогательных сфер R_max - O₂1₂. Минимальный радиус R_minберется наибольшим радиусом сферы, которую можно вписать в одну из заданных поверхностей, при этом пересекая другую поверхность.

Для построения промежуточных точек проводят несколько вспомогательных сфер (R_min<R<R_max). Эти сферы пересекают заданные поверхности по окружностям b и п. Окружности b и п, пересекаясь, дают дополнительные точки линии пересечения 3 и 4, проекции которых определяются вначале на π₂ (b₂∩п₂=3₂,4₂), а затем на плоскости π₁ как точки окружностей радиусами r.

Полученные точки (характерные и промежуточные) последовательно соединяют на фронтальной и горизонтальной проекциях.

На фронтальной проекции видна ближняя часть кривой (1₂-4₂-2₂) и не видна дальняя (1₂-3₂-2₂). Кривая пересечения поверхностей симметрична, значит (1₂-4₂-2₂)≡ (1₂-3₂- 2₂). На горизонтальной проекции видна часть кривой (... -3₁-1₁-4₁- ...), расположенная выше фронтальной проекции оси симметрии наклонного цилиндра. В этом случае границей видимости служат точки на горизонтальных проекциях очерковых образующих наклонного цилиндра.

4.2.5. Общие сведения о построение развертки.

Разверткой поверхности называется плоская фигура, полученная в результате совмещения поверхности с плоскостью. Построение разверток поверхностей имеет большое практическое применение при изготовлении различных изделий из листового материала. Это обшивка самолётов и судов, всевозможные резервуары и трубопроводы в нефтехимической и газовой промышленности, изделия швейной и кожевенной промышленности и т.д.

Рис. 17. Пример решения задачи методом сфер

Для построения развёртки используются ортогональные проекции поверхности. Связь между ними описывается инвариантным свойством сохранения площадей соответственных фигур. Это свойство влечёт за собой ещё такие свойства:

Ø длины соответственных линий поверхности и её развёртки равны,

Ø углы, образованные линиями поверхности, равны углам, составленным их образам на развёртке,

Ø прямая поверхности отображается на прямую развёртки,

Ø параллельные прямые поверхности отображаются на параллельные прямые развёртки.

Разработка наиболее простых и точных способов построения разверток необходима для изготовления тонкостенных изделий заданной формы и размеров. Чем рациональнее и точнее способ выполнения разверток и их раскроя, тем экономичнее технология изготовления изделий. При этом экономится листовой материал и рабочее время.

Теоретически точно развертываются поверхности многогранников, прямых круговых конусов и цилиндров. Приближенными развертками являются развертки поверхностей наклонных конусов и цилиндров, а развертки сфер являются условными.

В общем случае, построение любой развертки сводится к построению натуральной величины и формы элементов, составляющих поверхность.

4.2.6. Развертка пирамиды.

Для построения развертки пирамиды (рис. 18) необходимо найти натуральные величины ее боковых ребер и основания.

Основание пирамиды представляет собой треугольник, изображенный в натуральную величину на плоскости π₁.

Для определения натуральных величин боковых ребер воспользуемся способом прямоугольного треугольника, где S₀B₁=S₁B₁aS₂B₁ - натуральная величина SB. Аналогично находятся и другие натуральные величины ребер.

После определения натуральных величин ребер строим развертку пирамиды. Для этого на любом из ребер, например S₂A₀( или отдельно), строим треугольники (грани и основание) по трем известным теперь сторонам. Построение боковых граней заканчивается тем же ребром, с которого начинается построение развертки боковой поверхности пирамиды.

Нанесение линии пересечения на развертку производится отрезками прямых по характерным точкам (точкам излома) в случае пересечения пирамиды с многогранником. Если пирамида пересекается с поверхностью второго рода, то линия пересечения строится с использованием лекал по промежуточным точкам отрезков кривых, ограниченных точками излома. Для определения положения любой точки поверхности на развертке, например точки N, вначале находят положения проекций k₁ и k₂, прямой k, проходящей через вершину S и данную точку. Затем, прямую k наносят на развертку, при условии, что [А₀К₀]=[А₁К₁]. Далее, используя теорему Фалеса, определяют истинное положение точки N₀.

4.2.7. Развертка прямого кругового конуса.

Развертка прямого кругового конуса (рис. 19) представляет собой сектор круга, радиус которого равен длине образующей конуса b, а центральный угол а

,(2)

где R - радиус основания конуса.

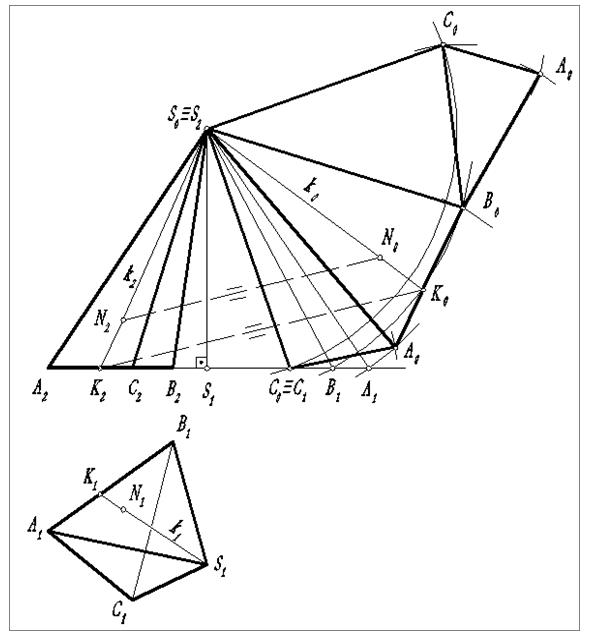
Рис.18. Построение развертки пирамиды

Нанесение линии пересечения поверхностей на развертку производится по точкам с использованием лекал. Для определения положения любой точки поверхности на развертке, например точки N., вначале находят положения проекций k₁и k₂ образующей k, которой принадлежит эта точка. Затем прямую k наносят на развертку при условии, что длина дуги A₀K₀ равна длине дуги 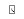A₁K₁. Далее, используя теорему Фалеса, определяют истинное положение точки N₀: ([K₀N₀] =m).

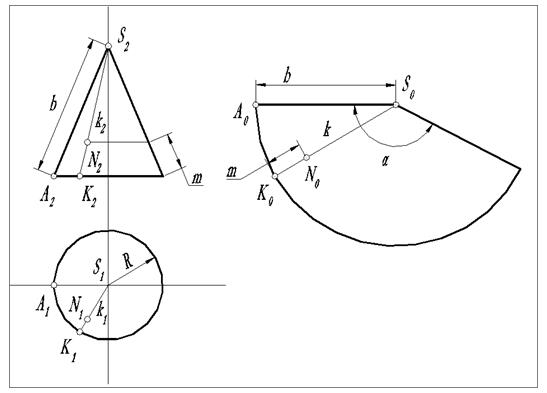
Рис.19. Нанесение проекции точки на развертку

Примечание. Развертку прямого конуса можно строить как развертку конической поверхности общего вида, т.е. в конус необходимо вписать правильную многогранную пирамиду.

4.2.8. Развертка конической поверхности общего вида,

Для получения развертки боковой поверхности наклонного конуса в него вписывают многогранную пирамиду. Чем больше граней у вспомогательной пирамиды, тем точнее развертка.

Примечание. Рекомендуется окружность основания конуса делить на 12 равных частей при R>25мм и на 8 - при R<25мм (R - радиус основания конуса).

Развертывание конической поверхности общего вида производится по схеме развертывания боковой поверхности наклонной пирамиды. Отличительной особенностью является то, что полученные точки боковой поверхности, описывающие окружность основания конуса, соединяются не прямыми, а кривой с помощью лекал.

Основание конуса на развертке изображается окружностью (в натуральную величину), касающейся в любой точке кривой боковой поверхности, описывающей основание.

Методика построения линии пересечения поверхностей на развертке конуса аналогична методике, описанной в пункте ’’Развертка пирамиды".

2.4.9. Развертка призмы.

В общем случае каждая грань призмы (рис. 20) имеет форму параллелограмма. В данном примере натуральная величина ребер определяется на плоскостиπ₂ а оснований - на плоскостиπ₁.

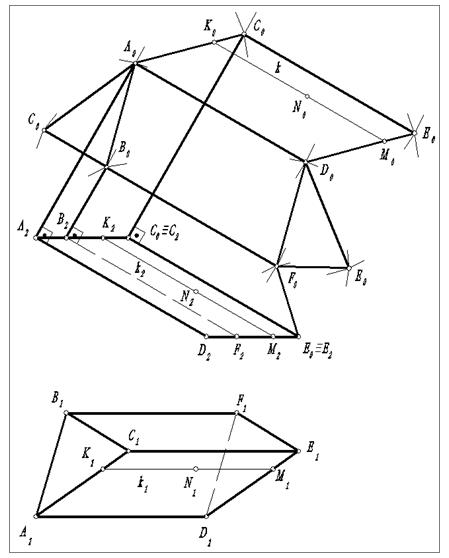
Рис. 20. Развертка призмы

Если в исходных данных призма занимает общее положение, то необходимо способом замены плоскостей преобразовать ее проекции так, чтобы грани призмы были, либо фронталями, либо горизонталями, а плоскости оснований - плоскостями уровней.

Развертку боковой поверхности делают методом раскатки - совмещают грани призмы с плоскостью проекций. Для этого все точки вращают в плоскостях, перпендикулярных проекциям ребер, а расстояния между ребрами берутся равными соответственно величинам сторон основания.

Нанесение линии пересечения на развертку производится отрезками прямых по характерным точкам (точкам излома) в случае пересечения призмы с многогранником. Если призма пересекается с поверхностью второго рода, то линия пересечения строится с использованием лекал по промежуточным точкам отрезков кривых, ограниченных точками излома.

Для определения положения любой точки поверхности на развертке, например точки N, вначале находят положения проекций k₁ и k₂ прямой k, параллельной боковым ребрам призмы и которой принадлежит эта точка. Затем, прямую k наносят на развертку при условии, что [A₀K₀]=[A₁K₁].Далее, используя [K₂N₂]=[K₀N₀], определяют истинное положение точки N₀.

4.2.10. Развертка прямого цилиндра.

Развертка боковой поверхности прямого цилиндра представляет собой прямоугольник (рис. 21), одна сторона которого равна образующей l, а другая - длине окружности основанияn

n=2πR, (3)

где R– радиус основания окружности.

Рис.21. Построение развертки цилиндра

Каждое основание цилиндра наносят в виде круга с радиусом R, касающегося в любой точке стороны п прямоугольника, описывающего его.

Нанесение линии пересечения поверхностей на развертку производится по точкам с использованием лекал. Положение любой точки поверхности на развертке, например N, определяется следующим образом. Вначале определяют проекции k₁ и k₂ образующей k, которой принадлежит точка N. Затем определяют положение этой образующей на развертке по условию, что отрезок [B₀K₀] равен длине дуги B₁K₁. Так как k₂=k, то положение точки N₀ на развертке определяется как [N₀K₂]= [N₂K₂]

Примечание. Развертку прямого цилиндра можно строить как развертку наклонного цилиндра, т.е. в цилиндр необходимо вписать правильную многогранную призму.

4.2.11. Развертка наклонного цилиндра.

Чтобы построить развертку цилиндра, необходимо вписать в него призму с достаточно большим числом граней и развернуть ее. Чем больше граней у вспомогательной призмы, тем точнее развертка.

Примечание. Рекомендуется окружность основания цилиндра делить на 12 равных частей при R>25mm и на 8 - при R<25mm (R - радиус основания цилиндра).

Развертывание цилиндрической поверхности общего вида производится по схеме развертывания боковой поверхности наклонной призмы. Отличительной особенностью является то, что полученные точки боковой поверхности, описывающие окружности оснований цилиндра, соединяются не прямыми, а кривыми линиями с помощью лекал.

Основания цилиндра на развертке изображаются окружностями (в натуральную величину каждое), которые касаются в любой точке кривой боковой поверхности, описывающей это основание.

Методика построения линии пересечения поверхностей на развертке наклонного цилиндра аналогична методике, описанной выше(см. “Развертка призмы”).

4.2.12. Развертка сферы.

Сферическая поверхность является неразвертываемой. Здесь можно говорить только об условном развертывании. На рис. 22 показан один из приемов построения. Поверхность “разрезают” несколькими плоскостями, проходящими через ось сферы, перпендикулярную π₁. Точность развертки зависит от числа плоскостей - чем больше плоскостей, тем точнее развертка. На рис.22 число таких плоскостей 12 (фронтальные проекции линий пересечения не показаны).

Дуги окружностей на плоскости π₁в лепестках развертки заменяют прямыми, касательными к этим дугам, например, прямая А₁В₁ заменяет дугу ав.

На плоскости π₂ 1₂7₂ делят на равные части: 1₂2₂=2₂3₂=...=6₂7₂ (чем больше частей - тем точнее развертка). Принимая точки 1₂ 2₂, 3₂,... за фронтальные проекции отрезков АВ, CD, EF, образующих лепестка развертки, строят их горизонтальные проекции A₁B₁,C₁D₁, E₁F₁,...

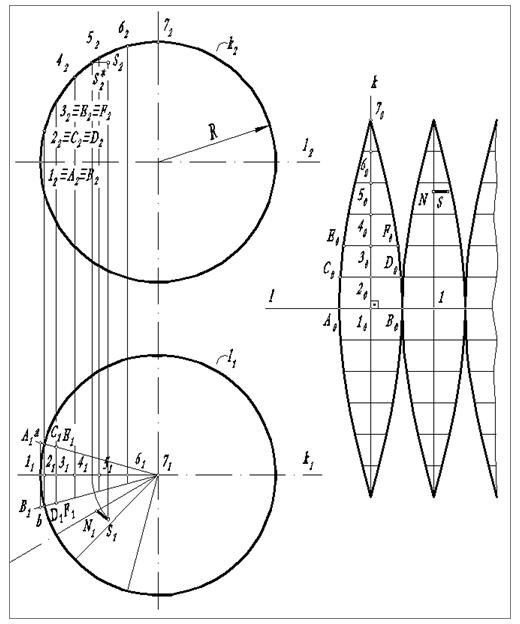
Рис. 22. Развертка сферы

На прямой l откладывают отрезок A₀B₀=A₁B₁и через его середину (точка 1₀) проводят перпендикуляр k. На этом перпендикуляре откладывают отрезки [1₀2₀]= 1₂2₂, [2₀3₀]= 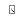2₂3₂, [3₀4₀]= 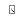3₂4₂,[4₀5₀]= 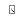4₂5₂, [5₂6₂]= 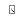5₂6₂и[6₂7₂]= 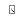6₂7₂ и через полученные точки 2₀, 3₀, 4₀, 5₀, и 6₀ проводят отрезки [C₀D₀]=[C₁D₁]_, [E₀F₀]=[E₁F₁]и т.д., параллельные прямой A₀B₀, при этом точки 2₁≡2₀, 3₁≡3₀ и т. д.

По лекалу через полученные точки А₀,D₀,F₀, ... ,7₀и В₀ С₀„ E₀... , 7₀проводят кривые. В результате получается приближенная развертка половины лепестка сферической поверхности. Далее, используя эту часть лепестка, строят недостающую часть развертки.

Примечания.

1. Окружность сферы рекомендуется делить на 12 равных частей (лепестков) при R>25mmи на 8 - при R<25mm (R- радиус сферы).

2. Дугу 1₂7₂ следует делить не менее чем на 4 равные части (6, 8, 10 или 12 частей).

Построение линии пересечения поверхностей на развертке производится по ее точкам с использованием лекал.

Для нахождения положения точки на развертке, например S, определяют ее положение относительно экватора ( 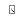1₂S*₂) и центральной линии сегмента [S₁N₁], в котором она находится. Далее полученные значения этих величин наносят на развертку, т.е. [1N]- 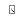1₂S₂* и [SN]=[S₁N₁].