Пример решения РГР № 3

4.3.1. Построение исходных данных.

Вертикальную ось симметрии полусферы размещаем посередине между левой внутренней рамкой формата и левой границей основной надписи (приложение 4, рис. 96, 97). По исходным данным строим горизонтальные проекции полусферы и прямой призмы в масштабе М 1:1 (рис. 23). Проводим ось проекций x и используя вертикальные линии связей наносим фронтальные проекции этих тел.

4.3.2. Построение линии пересечения тел.

Линия пересечения полусферы и прямой призмы будет пространственная замкнутая ломаная линия, состоящая из отрезков кривых второго порядка. Точка излома линии пересечения это точки встречи ребер призмы с поверхностью полусферы, а отрезки кривых являются линиями пересечения граней призмы с поверхностью полусферы.

Исходя из анализа формы и взаимного расположения тел, для построения линии пересечения, целесообразно использовать способ вспомогательных плоскостей. В качестве поверхности посредника выбираем горизонтальную плоскость уровня α. Сечениями, плоскостью посредником α, будут являться:

- для полусферы - половина круга;

- для прямой призмы – прямоугольник.

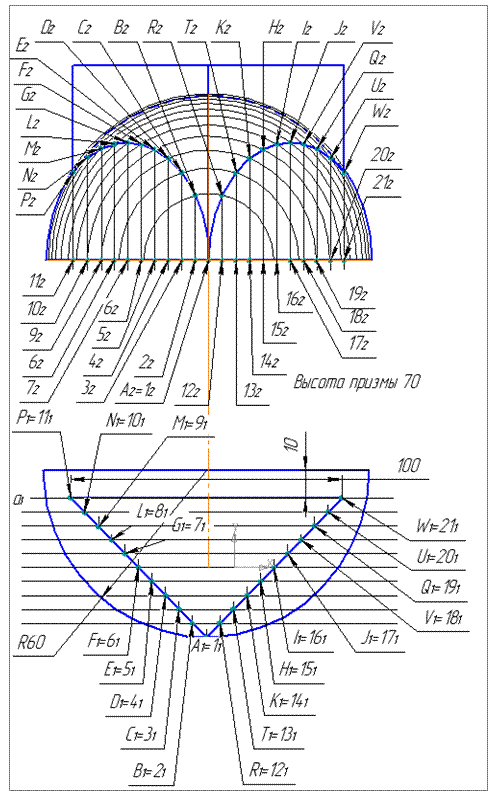
Рис. 23. Построение линии пересечения полусферы и прямой призмы

Точки пересечения линий, ограничивающих эти сечения, принадлежат линии пересечения тел. Меняя положения плоскости посредника α набираем необходимое количество точек для построения линии пересечения. Положения перемещения плоскости α показано перемещением ее проекции α₁, а сечения тел ограничивающими линиями. Проекции точек A, B, C, D, E, F, G, L, M, N, P, R, T, K, I, J, V, Q, U и Wпересечения линий сечения тел являются точками линии пересечения тел. Горизонтальная проекция линии пересечения совпадает с горизонтальным очерком прямой призмы. Фронтальную проекцию строят с учетом ее видимости с использованием лекал по точкам A₂, B₂, C₂, D₂, E₂, F₂, G₂, L₂, M₂, N₂, P₂, R₂, T₂, K₂, I₂, J₂, V₂, Q₂, U₂ и W₂. Обводку построения линии пересечения тел производят с учетом видимости тел относительно друг друга.

4.3.3. Построение развертки одного из тел.

Согласно задания развертку можно проводить, как для полусферы, так и для прямой трехгранной призмы. Рассмотрим построение развертки прямой призмы (рис. 24).

Боковая поверхность призмы состоит из прямоугольников, а основания представляют собой треугольники. Натуральные величины сторон прямоугольников и треугольников определены по условию задания (рис. 23), т.к. ребра призмы являются горизонтально-проецирующими прямыми, а основания – плоскостями уровней.

За начало отсчета выбираем ребро призмы, проходящее через точку 1. Направление разворачивания выбираем по часовой стрелке. Последовательно в натуральную величину строим прямоугольники граней боковой поверхности призмы в порядке их появления. Затем, используя принцип построения треугольника по трем известным сторонам, достраиваем основания призмы.

Построение линии пересечения тел на развертке начинают с нанесения точек 1.2.3.4.5.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20 и 21, реальное положение которых определяется на горизонтальной проекции призмы. Через эти точки проводят образующие боковой поверхности призмы (эти образующие будут в натуральную величину). Учитывая равенство отрезков [B2]=[B₂2₂], [C3]=[C₂3₂], [D4]=[D₂4₂], [E5]=[E₂5₂], [F6]=[F₂6₂], [G7]=[G₂7₂], [L8]=[L₂8₂], [M9]=[M₂9₂], [N10]=[N₂10₂], [P11]=[P₂11₂], [R12]=[R₂12₂], [T13]=[T₂13₂], [K14]=[K₂14₂], [H15]=[H₂15₂], [I16]=[I₂16₂], [J17]=[J₂17₂], [V18]=[V₂18₂], [Q19]=[Q₂19₂], [U20]=[U₂]=[U₂20₂],и [W21]=[W₂21₂] на соответствующих образующих определяют положения точек A, B, C, D, E, F, G, L, M, N, P, R, T, K, I, J, V, Q, U и W. По полученным точкам, с использованием лекало, строят линию пересечения тел.

Обводку развертки осуществляю с учетом видимости тел (линии пересечения).

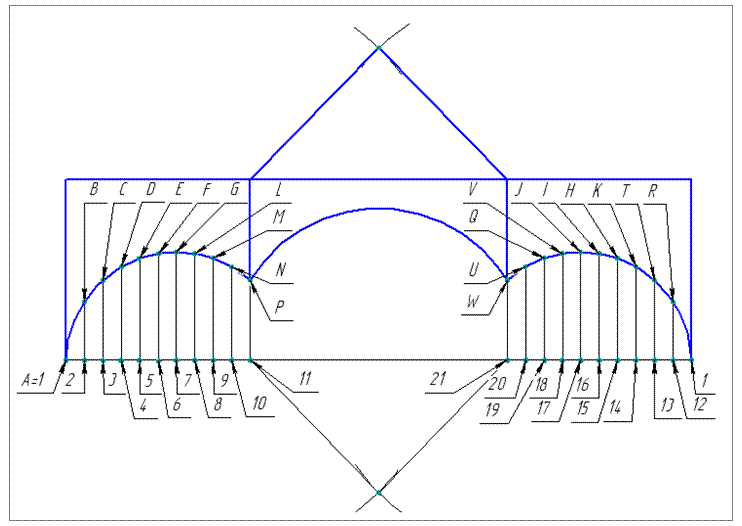
Рис. 24. Развертка призмы с нанесением линии пересечения

Вопросы для самоконтроля

1. В чем заключается общий способ построения взаимного пересечения двух поверхностей?

2. Что собой представляет линия пересечения двух многогранников?

3. Что собой представляет линия пересечения многогранника с поверхностью второго рода?

4. Что собой представляет линия пересечения двух поверхностей второго рода?

5. В чем сущность способа вспомогательных секущих плоскостей в построении линии пересечения двух поверхностей?

6. Когда можно использовать вспомогательные сферы при построении линии пересечения поверхностей?

7. В чем заключается сущность построения развертки пирамиды?

8. Какие допущения принимаются при построении развертки прямого и наклонного конусов?

9. В чем заключается сущность метода раскатки при построении развертки призмы?

10. Какие допущения принимаются при построении развертки прямого и наклонного цилиндров?

11. В чем заключается сущность методики построения развертки сферической поверхности?