Необходимые сведения

Поверхность конуса вращения определяется уравнением 2-го порядка

, (1)

значит, и сечением конуса могут быть кривые 2-го порядка, т.е. окружность, эллипс, парабола или гипербола.

В начертательной геометрии тип кривой 2-го порядка может быть определен следующим образом:

Ø Если секущая плоскость параллельна двум образующим конуса, то сечение будет гипербола. Обе ветви гиперболы можно получить, если конус будет иметь две полы.

Ø Если секущая плоскость параллельная одной образующей конуса, то сечением будет парабола.

Ø Если секущая плоскость пересекает все образующие, то сечением будет эллипс.

Ø Если секущая плоскость перпендикулярна к оси вращения конуса, то сечением будет окружность.

В инженерной графике секущие плоскости принято изображать в виде утолщённой разомкнутой линии, в начале и конце которой размещают прописные буквы русского алфавита, а само сечение сопровождается надписью, по типу А-А.

На рис. 9 плоскость А-А проходит параллельно двум образующим конуса (S-1 и S-2) и поэтому пересекает конус по гиперболе. Слева изображена истинная величина сечения А-А и 3-х мерное изображение конуса с сечением А-А.

На рис. 9 плоскость Б-Б проходит параллельной правой очерковой образующей S-3 конуса, поэтому сечением является парабола, истинная величина которой показана справа с сопровождающей надписью Б-Б. Ещё правее и ниже дано 3-х мерное изображение конуса, усеченного плоскостью Б-Б.

На рис. 9 плоскость В-В пересекает все образующие верхней полы конуса. Значит, сечением будет являться эллипс. Истинная величина сечения размещена справа с надписью В-В. Ещё правее и чуть выше показана 3-х мерная модель конуса, усечённого плоскостью В-В.

На рис 9 основания конуса перпендикулярны оси конуса OS и поэтому являются окружностями, горизонтальные проекции которых совпадают.

Если секущая плоскость проходит через вершину S конуса и пересекает его, то понятно, что в сечении будут две прямые (образующие конуса). Если секущая плоскость проходит через S и не пересекает образующие, сечением будет точка S. На рис. 9 сечения А-А, Б-Б, В-В и от плоскости b построены в натуральную величину и размещены в проекционной связи с секущей плоскостью.

На правой части рисунка изображены фронтальная и горизонтальная проекции того же конуса. Но здесь показаны приёмы получения в сечении гиперболы. Для этого через фронтальную проекцию S₂ вершины S под любым углом проводим проекции образующих S-1 и S-2 конуса, лежащих во фронтально проецирующей плоскости. Затем параллельно плоскости этих образующих проводим фронтальный след a₂ плоскости a сечения. Строим горизонтальную проекцию гиперболы, опорными точками которой являются точкиА, С и вершина В. Понятно что эта проекция гиперболы не определяет истинной величины сечения.

Ещё один вариант построения сечения в виде гиперболы получается, если секущая плоскость b будет параллельна фронтальной плоскости проекций, так как в этом случае плоскость b параллельна двум образующим – S-3, S-4. Фронтальная проекция гиперболы (Dи Fопорные точки сечения, а E – вершина гиперболы) есть истинная величина сечения.

Строить проекции сечения поверхности плоскостью можно по-разному, в зависимости от положения секущей плоскости относительно плоскостей проекций.

Ø Если секущая плоскость общего положения, то для упрощения алгоритма решения используют способы преобразования эпюра: способ замены плоскостей проекций, способ плоскопараллельного перемещения или способ вращения.

Ø Если секущая плоскость проецирующая, то в этом случае одна из проекций вырождается в прямую, совпадающую со следом-носителем проекций, а вторую проекцию сечения строим любым удобным способом, т.е. способом плоскостей уровня или способом определения точек пересечения образующих конической поверхности с секущей плоскостью.

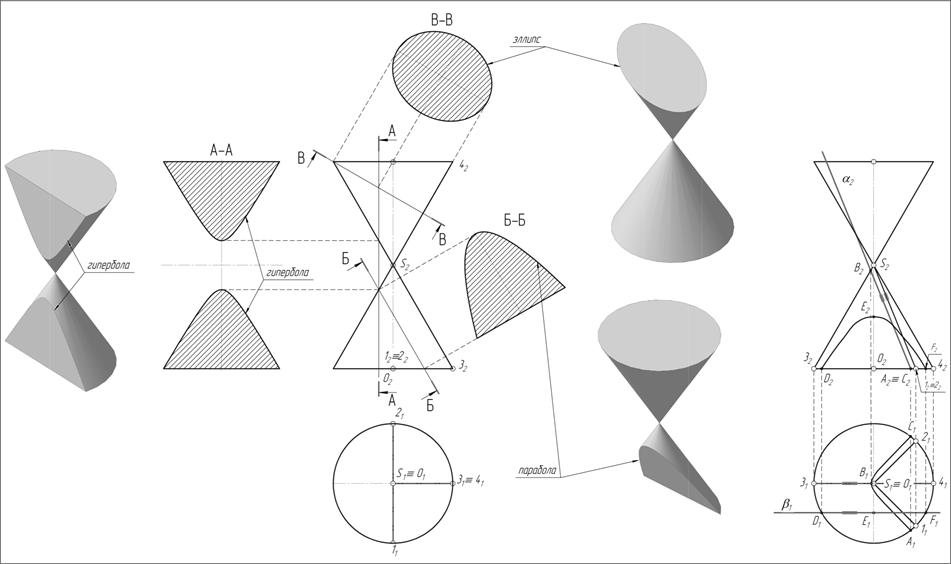
Рис. 9. Конические сечения

Натуральная величина сечения прямого кругового конуса проецирующей плоскостью строится по точкам, положение которых определяется с использованием:

- способа замены плоскостей проекций;

- способа вращения;

- способа

- свойств прямых частного положения.

Не зависимо от применяемого метода, суть решения сводится к переводу проецирующей плоскости сечения в положение плоскости уровня.

Учитывая, что при решении РГР № 2 необходимо соблюдать требования по компоновке чертежа, то наиболее подходящим является способ плоскопараллельного переноса.

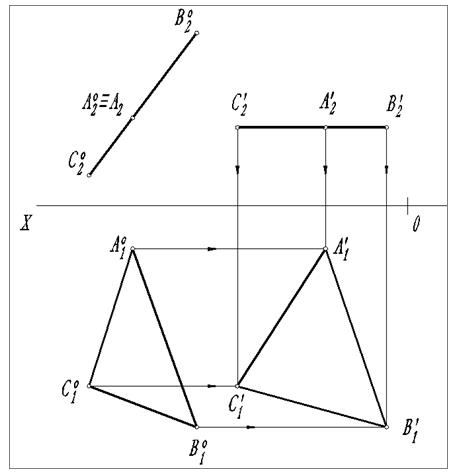
Рис. 10. Плоскопараллельный перенос

Суть данного способа заключается в следующем (рис. 10). Одну из проекций геометрического образа, не изменяя ее вида и величины, перемещают параллельно самой себе и поворачивают на необходимый угол. Другую проекцию перемещают только параллельно самой себе. Затем, используя линии перемещения и линии связей, строят новую проекцию геометрического образа.