Порядок выполнения работы. 2.2.1. По координатам точек А, В, С, D и Е построить проекции плоскости а, заданной треугольником ABC и отрезок [DE] прямой l.

2.2.1. По координатам точек А, В, С, D и Е построить проекции плоскости а, заданной треугольником ABC и отрезок [DE] прямой l.

Для этого, на поле чертежа (рис. 5) наносят оси пересечения плоскостей проекций OX, OY, OZ (точка "О"- начало координат) и по заданным координатам определяют положение точек А, В, С, D и E.

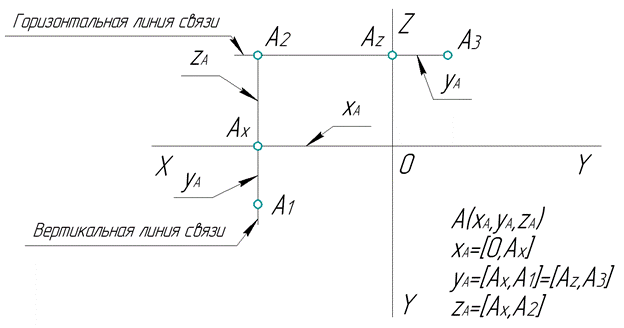
Рис. 5. Эпюр точки А

Следует помнить, что горизонтальная и фронтальная проекции точки лежат на одной прямой, перпендикулярной к оси ОХ (и параллельной осям OYи 0Z), а фронтальная и профильная проекции на прямой, перпендикулярной к осям OY и OZ (и параллельной оси ОХ). Эти линии называются вертикальной и горизонтальной линиями связи.

Соединив соответствующие проекции точек А, В и С, получим проекции треугольника ABC на плоскостях проекций π₁, π₂ и π₃. Аналогично, соединив проекции точек D и E,получим проекции отрезка [DE]прямой l (рис. 6).

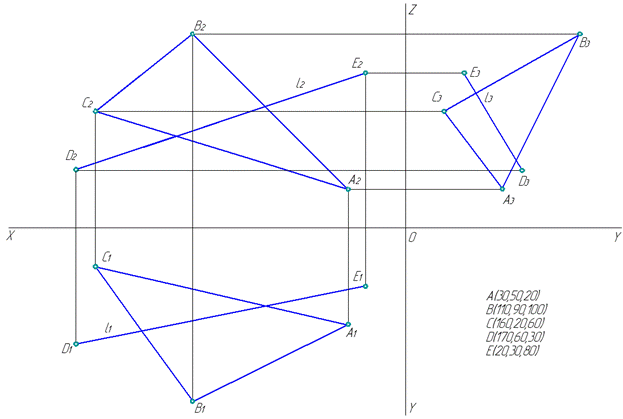
Рис. 6. Построение проекций плоскости и прямой

2.2.2. Определить точку встречи N прямой l с плоскостью а, заданной треугольником АВС (рис. 7).

Для этого, заключив прямую l в горизонтально-проецирующую или фронтально-проецирующую плоскость β (на рис.3 использована фронтально-проецирующая плоскость) и находят линию пересечения плоскостей а и β.

Вторая проекция линии пересечения плоскостей а и β совпадает с вырожденной проекцией плоскости β₂, которая проходит через точки 1₂ и 2₂ плоскости а. Недостающую проекцию этой прямой строят по принадлежности прямой плоскости.

Точка пересечения горизонтальной проекции прямой l₁ и первой проекции линии пересечения плоскостей а и β является горизонтальной проекцией точки встречи N₁ прямой l с плоскостью а. Недостающие проекции точки встречи N₂ иN₃ определяются по принадлежности точки N прямой l с использованием вертикальной и горизонтальной линий связей.

Рис. 7. Нахождение точки встречи прямой с плоскостью

Следует отметить, что точка встречи прямой l и плоскости а не обязательно должна лежать в пределах плоскости, ограниченной треугольником АВС (см. рис.92,93).

2.2.3. Определить видимость прямой l относительно плоскости а, ограниченной треугольником АВС.

Видимость определяется с помощью конкурирующих точек.

Видимость проекции прямой l на плоскости проекций π₁. Возьмем две скрещивающие прямыеlи АВ (рис. 4). Обозначим точку пересечения их проекций на π₁ точками 3₁и 4₁, при условии, что точка 4 принадлежит прямой 1, а точка 3 стороне АВ треугольника АВС. По принадлежности точки прямой находим недостающие проекции точек 3₂ и 4₂. Располагаем взгляд в бесконечности от оси ОХ в плоскости проекций π₂ и смотрим (на рис. 4 символ «↓» - направление взгляда), какая проекция встречается первой. Проекция точки 3₂ встречается первой. Это означает, что проекция точки 3₁ видима, а проекция точки 4₁ не видима (закрыта проекцией точки 3₁). Следовательно, отрезок [3₁N₁] проекции прямой 1₁ будет закрыт, по видимости, проекцией треугольника А₁В₁С₁.

Видимость проекций на плоскости проекций π₂. Возьмем две скрещивающие прямые l и АС (рис. 8). Обозначим точку пересечения их проекций на π₂ точками 1₂ и 5₂ , при условии, что точка 5 принадлежит прямой l, а точка 1 принадлежит стороне АС треугольника АВС. По принадлежности точки прямой находим недостающие проекции точек 1₁ и 5₁. Располагаем взгляд в бесконечности от оси ОХ в плоскости проекций π₁ и смотрим (на рис. 8 символ «↑» - направление взгляда), какая проекция встречается первой. Проекция точки 5₁ встречается первой. Это означает, что проекция точки 5₂ будет видима, а проекция точки 1₂ будет не видима (закрыта проекцией точки 5₂).

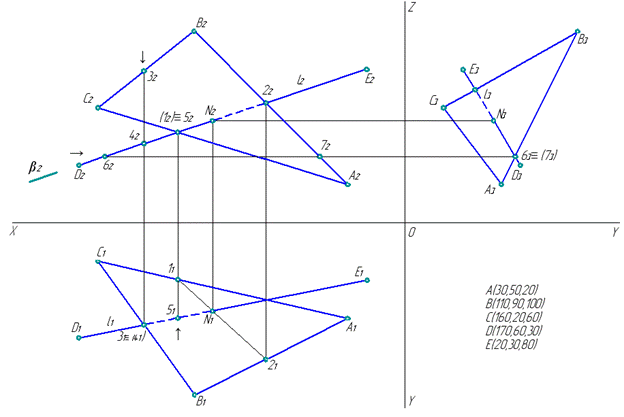
Рис. 8. Определение видимости прямой

Учитывая принадлежность точек 1 и 5, имеем, что отрезок [2₂N₂] проекции прямой l₂ будет закрыт проекцией треугольника А₂В₂С₂.

Видимость проекции прямой l на плоскости проекций π₃. Возьмем две скрещивающие прямые l и АВ (рис. 8). Обозначим точку пересечения их проекций на π₃ точками 6₃и 7₅, при условии, что точка 6 принадлежит прямой 1, а точка 7 стороне АВ треугольника АВС. По принадлежности точки прямой находим недостающие проекции точек 6₂ и 7₂. Располагаем взгляд в бесконечности от оси ОZ в плоскости проекций π₂ и смотрим (на рис. 8 символ «→» - направление взгляда), какая проекция встречается первой. Проекция точки 6₂ встречается первой. Это означает, что проекция точки 6₃ видима, а проекция точки 7₃ не видима (закрыта проекцией точки 6₃). Следовательно, отрезок проекции прямой 1₃от точки N₃до стороны В₃С₃.будет закрыт, по видимости, проекцией треугольника А₃В₃С₃.

Вопросы для самоконтроля

1. Как определить по координатам расположение точки на эпюре Монжа?

2. Какая проекция точки располагается на оси 0Х,если точка лежит в плоскости π₁, и какая, если точка находится в плоскости π₂.

3.Как расположен отрезок прямой, если концевые его точки имеют:

- равные координаты z;

- равные координаты y;

- равные координаты x?

4. Какие точки называются конкурирующими?

5. Какие прямые проецируются в натуральную величину на плоскостях проекций π₁, π₂ и π₃?

6.Как проецируются на плоскостях проекций π₁, π₂ и π₃ фронтали, горизонтали и профильные прямые?

7.Как найти точку, делящую отрезок прямой в заданном отношении?

8. Как проецируется на плоскостях проекций π₁, π₂ и π₃ прямой

угол, если одна из его сторон является фронталью, горизонталью или профильной прямой?

9. Как определяются точки встречи (следы) прямой с плоскостями проекций π₁, π₂ и π₃?

10.Как определить следы плоскости общего положения на плоскостях проекций π₁, π₂ и π₃?

11.Как на чертеже определяется видимость прямой относительно плоскости общего положения, заданной геометрической фигурой?

12. Как на чертеже провести плоскость, параллельную заданной?

13.Как на чертеже построить плоскость, перпендикулярную прямой общего положения?