Спектральный состав импульсов

Периодическая последовательность импульсов представляет собой несинусоидальное периодическое колебание. Одиночный импульс не является исключением, его можно представить как последовательность импульсов с бесконечным периодом (Т стремится к бесконечности). Периодическое несинусоидальное колебание может быть представлено бесконечным тригонометрическим рядом Фурье, содержащим постоянную состояния и гармонические колебания. Результат воздействия на схему каждой составляющей определяется сравнительно просто, пользуясь принципом наложения можно действия импульса на цепь заменить суммарным действием всех его составляющих. Часто используется следующая формула ряда Фурье:

f(t)=A0\2+A1*cosω1t+ A2*cos2ωt+…+ An*cos*nωt+…+ B1*sinω1t+ B2*sinω2t+…+ Bn*sin*ωt+…

где, n=1,2,3 ω=2πf1 f1=1\T

Совокупность гармоник составляют данное несинусоидальное колебание представленное, графическим изображением спектра называется спектральной диаграммой. На спектральной диаграмме каждая гармоника изображается вертикальной линией, длина этой линии пропорционально амплитуде гармоники, а ее положение на оси абсцисс определяется частотой гармоники. Спектральная диаграмма дает наглядное представление о зависимости амплитуд гармоник то ее частоты

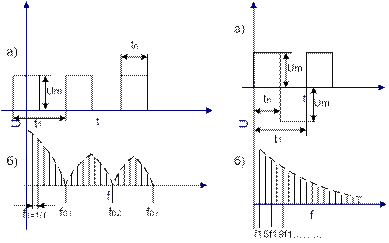
f01=1\tn, f02=2\tn. а) – временные диаграммы, б) – спектральные диаграммы

С увеличением номера гармоники их амплитуда имеет тенденцию к уменьшению. Чем короче импульс, тем шире его спектр. Симметрия его относительно начало координат левый рисунок приводит к тому, что в разложении не будет синусоид гармоники постоянной составляющей и отсутствую гармоники четных номеров, обусловленные симметрией относительно оси абсцисс. Поэтому разложение будет содержать синусоидальные составляющие нечетных номеров. Таим образом, в составе спектра содержит бесконечное количество синусоидальных гармоник амплитуд, которых обратно пропорциональны номеру гармоник, с увеличение они уменьшаются по гиперболическому закону (правый рисунок).

Дискретное представление непрерывных величин. Основные понятия и определения

Цифровым измерительным прибором называют измерительный прибор, автоматически вырабатывающий дискретный сигнал измерительной информации показаний, которое представлено в цифровой форме. Под дискретным сигналом понимают сигнал у которого информация заложена не в значениях величины используемой для передачи этой информации, а в соответствии ей количестве сигнала их взаимного расположения и тому подобному, причем дискретный сигнал в отличии от непрерывного может иметь только определенное число значений. Система определенных правил или комбинаций используемых для определения информации посредством цифр или дискретных сигналов называются кодом. Дискретные сигналы в отличие от непрерывных могут иметь лишь конечное число значений определяемых выбранным кодом. Цифровая форма по сравнению с аналоговой ускоряет считывание и уменьшает вероятность субъективных ошибок. Структурная схема цифровых приборов иметь существ различия. Рассмотрим принцип действия универсального цифрового прибора

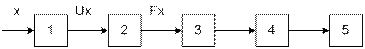- обобщенная структурная схема ЦИП

где 1 предварительный преобразователь,2 АЦП, 3 декадный счетчик, 4 преобразователь входа (дешифратор) 5 цифровое отсчетное устройство.

Предварительный преобразователь преобразует измеряемую величину произвольной физической природы, в пропорциональное напряжение постоянного тока или соответствующий интервал времени (временной интервал). АЦП осуществляет преобразование напряжения или интервала времени в дискретный сигнал измерительной информации. Процесс преобразования включает дискретизацию, квантование и цифровое кодирование. Под дискретизацией понимают такую операцию в результате которой аналог входная величин х(t) сохраняет свои значения лишь до определенных моментов времени называемых моментами дискретизации. (Рисунок ниже Б) Интервал времени дельта т между двумя последовательными моментами дискретизации называют шагом дискретизации.

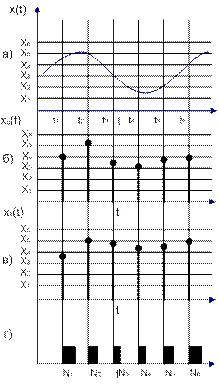
Процесс образования дискретного сигнала измерительной информации: а – измеряемая величина, б -дискретизация, в – квантование дискретных значений, г – цифровое значение квантованных значений (унитарный код). Под квантованием понимают операцию замены истинных мгновенных значений измеряемой величины ближайшими фиксированными значениями из известной совокупности дискретных величин, называемых уровнями квантования. На рисунке в уровни квантования представлены значениями х1, х2 и т.д. в цифровых приборах совокупность уровней квантования образуют в результате масштаб деления напряжения меры ЭДС и поэтому их цифровое значение с высокой степенью точности. Разность ∆х между уровнями называют интервалами квантования. Затем рисунок Г квантование величины преобразуют пропорции число в унитарный ряд. Соответственно в отчетном устройстве этот код преобразуется в сигналы удобные для передачи или зрительного восприятия. Операция дискретизации и квантования могут быть источниками погрешности присущих цифровым приборам. Так, например операция дискретизации при чрезмерно большом шаге ∆t может повлечь за собой потерю части исходной информации.

Информационная емкость непрерывного сигнала. Теорема отсчета (теорема Котельникова).

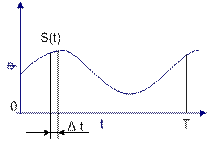
Таким образом, вся содержащаяся в непрерывном сигнале информация может быть определена совокупностью выбора взятых из сигнала в дискретные равноотстоящие моменты времени. Величина интервала ∆t между соседними выборками зависит от наивысшей частоты в спектре сигнала: чем больше эта частота, тем меньше должен быть интервал. Если наивысший интервал меньше Fm, то интервал между выборками не должен превышать1\2Fm. Это важное положение основывается на теореме Котельникова: если наивысшая частота в спектре функции S(t) меньше чем Fm, то функция S(t) полностью определяется последовательность своих значений в моменты отстоящей друг от друга не более чем 1\2Fm секунд. (второе название: теорема отсчетов)/ при полной длительности сигнала т число выборок равно N.

N=T\∆t+1=2FmT+1, т.к. обычно 2FmT»1, то N≈2FmT

Во вторых бесполезно пытаться измерить сколь угодно малое изменении выборки, так как помехи всегда присутствующие, в реальном сигнале ограничивая точность измерения. Минимальные изменения сигнала обнаруженные измерительным устройством может быть в первом приближении приравнено к уровню шумов (канала связи, самого измерителя). Таким образом, при эффективном напряжении помехи σ (нормальный случайный процесс) и эффективном напряжении Uс σ число различимых уровней смеси (сигнал плюс шум) может быть представлено в виде отношения:

∆=(√U²cэфф+σ²)/ σ=√Рсигн+Рпомехи/Рпомехи

Рс= U²cэфф Рп= σ L – число различаемых уровней

где Рс – средняя мощность сигнала, Рм – средняя мощность помехи (при сопротивлении цепи 1Ом).

По своей информативной емкости непрерывный сигнал может быть приравнен к дискретной по времени последовательности выборок, каждая из которых, может принимать одно из конечного числа конечных значений. Если заданы параметры сигнала (мощность сигнала, длительность, Fm), то получим следующее выражения для информативности непрерывного сигнала:

(T/∆t)log₂L=2FmTlog2√Pc+Pп/Рп=FmTlog₂(Pc+Pп/Рп) при 2FmT»1

где log₂L – информационная емкость в двоичных единицах

При спектре сигнала от 0 до Fm, величины Fm можно рассматривать как ширину спектра омега в Гц, тогда скорость передачи информации равна:

С=ωlog₂(Pc+Pп/Рп), двоич.ед./сек

Операция квантования аналоговой величины сопровождается появлением случайной погрешности округления. Если полагать, что случайная погрешность округления ∆ равномерно распределены в пределах интервала (-∆х/2÷∆х/2), то среднеквадратичное значение погрешности квантования можно определить по формуле:

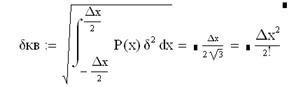
Отметим что погрешность квантовая пропорционально квадрату интервала ∆х. Практически цифровое кодирование квантованных значений осуществляется в 2 этапа. В начале, Хi преобразует пропорциональное число кратковременных импульсов в унитарный код, а затем исходный код преобразуется в двоично-десятичный код (8-4-2-1). Последнее упрощает представление измерительного информации в наиболее естественной цифровой форме, а также облегчает возможность сопряжения прибора с информационно измерительной системой, АСУТП. Декадные счетчики осуществляют преобразование исходного кода в двоично-десятичный. Основным элементом счетчика служит триггерные ячейки. Цифровые приборы обычно содержат от трех до 9 декадных счетчиков. Основной характеристикой счетчика определяющая предельную скорость прямого счета импульсов является быстродействие. Предельная частота переключения серийных счетчиков 500 МГц. В ряде измерительных приборов декадные счетчики служат основным элементом устройств деления частоты, в том числе и частоты гармонических колебаний. Пересчетная схема с управляемыми коэффициентами деления используют для формирования следования и длительности импульсов также для устройства временной задержки. Дешифратор: осуществляет преобразование двоично-десятичного кода, который представлен информацией на выходе декадного счетчика, в сигнал входа, используя цифровыми индикаторами последующего цифрового отсчетного устройства. Цифровое отсчетное устройство служит для предоставления результата измерений в виде десятичного числа удобного для восприятия оператора. Отсчетное устройство состоит из коммутатора и знаковых индикаторов. В качестве последних применяются газоразрядные индикаторные лампы, цифробуквенные индикаторы на основе светодиодов.