Погрешности аналого-цифровых преобразователей.

Процесс преобразования аналоговой величины х в цифровую М состоит в определение того к какому из уровня квантования ближе всего расположено данное значение непрерывной измеряемой величины. При этом неизбежно возникают погрешности. Если предположить, что уровни квантования заданны с идеальной точностью, а определение уровня, к которому ближе всего расположено истинное значение величины выполняется безошибочно, то остается не исключенной только методическая погрешность вызванная округлением. Обычно ее называют погрешность квантования. ∆к=х-М∆х – абсолютное ее значений, где М∆х - то значение до которого производится округление

Возможные значения величины х округляемые до М∆х расположены в зоне от М∆х-∆х/2 до М∆х+∆х/2, следовательно диапазон значений погрешности ∆к=-∆х/2 ÷ ∆х/2.

Измеряемая величина всегда случайная следователь погрешность ∆к тоже случайна. Доказана то что если квант ∆х много меньше диапазона шкалы измерений (типичный для измерений), то закон распределения погрешности ∆к почти не зависит от закона распределения измеряемой величины х и приближается к равномерному. Плотность вероятности погрешности

P(∆х)=0 при ∆х<-∆х/2

P(∆х)=1/∆х при -∆х/2≤∆к≤∆х/2

P(∆х)=0 при ∆к>∆х/2

Допущение о том, что уровни квантования задаются без погрешности, а устройство сравнения, определяющее принадлежность х к той или иной зоне работает безошибочно, было принято выше чисто условно. Теперь от него следует отказаться и учесть инструментальные погрешности. Сначала учтем погрешность вносимую устройством сравнения, логика его работы такая: если величина х больше М∆х-∆х/2, но меньше М∆х+∆х/2, то ей соответствует число М. но если устройство сравнения неидеально (обладает дрейфом нуля, наличие шумов), то не исключена, например, возможность такого события: величина х меньше М∆х-∆х/2, устройство сравнения выдает что она больше. Точно также не исключена возможность такого решения, когда величина х больше М∆х+∆х/2, ошибочно принято за величину М∆х+∆х/2. Величина х может оставаться постоянной при многократных повторениях цифрового преобразования то она будет априори в 70% случая зачисляться в примыкающую к уровню с номером М, в 25% к М+1, а в 5% даже в более дальнюю зону, примыкающую к номеру М+2. Из приведенных рассуждений видно, что при неидеальном устройстве сравнения погрешность цифрового преобразования может выйти за пределы + ∆х/2. Закон распределения суммарной погрешности отличается от 4. Чтобы ее найти нужно знать закон распределения дрейфа нуля устройства сравнения ∆с. Р(∆с) – дрейф нуля.

Закон распределения суммарной погрешности нужно определять как композицию двух законов распределения: Р(∆к) и Р(∆с). Для этого требуется громоздкие вычисления из теории вероятностей и математической статистики. Но во многих случаях можно ограничиться задачей отыскания числовых значений суммарной погрешности. Особенно часто используется в качестве критерия точности среднее и среднеквадратическое значение суммарной погрешности.

Теперь рассмотрим вторую инструментальную погрешность, вызываемую неточным заданием уровней квантования М∆х. Если погрешность ∆у задания уровня М∆х случайна, то результат ее суммировании ∆к и ∆с можно определить отыскав композицию двух законов распределении с третьей Р(∆у). Примем для простоты что закон распределения Р(∆у) один и тот же для уровней с любым номером М, тогда все результаты которые будут получены ниже можно использовать для любой точки шкалы преобразовании. Возьмем в качестве числовых характеристик рассматриваемых законов распределения их средние значения (математическое ожидание), определяемые по формуле

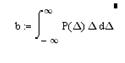(4)

σ - показывающая степень их рассеивания относительно средних значений и определяется по формуле

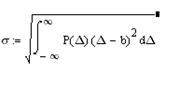(5)По поводу данной формулы следует сделать особую оговорку, дело в том, что можно рассматривать два вида среднеквадратичных значений случайной величины. Первая из них подсчитывается по 7 и показывает меру рассеивания относительно среднего значения b. Второе вычисляется по формуле 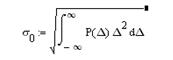(6) и показывает меру рассеивания той же величины относительно нуля. Между этими критериями существует простая связь σ₀²= σ²+b² . (7)

Для случайных величин, у которых среднее значение b=0, критерии σ- σ₀совпадает. Случайные погрешности статистически независимы, поэтому для определения средней и среднеквадратической суммарной погрешности ∆Σ можно воспользоваться известными формулами из теории вероятностей.

bΣ=bk+bc+by (8) σΣ =√σк²+σс²+σу² (9)

Значения bс, σу, bу, относящиеся к инструментальным погрешностям, зависят от свойств конкретных устройств сравнения и заданий уровней. Значения bк и σк, относящиеся к методической погрешности, можно установить на основе закона распределения. При bk=0 σк=∆х/2√3 (10).

В некоторых устройствах цифрового преобразования зона округления примыкающей к уровню квантования с номером М может располагаться несимметрично относительно этого уровня. Например, она может располагаться по одну строну от уровня, т.е. от М∆х до М∆х+∆х, тогда закон распределения Р(∆к) отличается от выражения (3) и значения bк не равно нулю. Существуют преобразования, в которых погрешность квантования возникает дважды во время одного преобразования. Это бывает тогда когда начало отсчета величины х и уровней квантования М∆х не совмещены между собой. В таких случаях погрешность ∆к следует учитывать дважды и соответственно рассматривать два средних значения.

Каждый из формулы 8,9 взятый в отдельности не дает правильного представления о погрешности преобразования: среднее значение bΣ может быть малым, а разброс погрешностей относительно среднего значения большим. И наоборот, возможен случай, когда величина σΣ мала, т.е. разброс погрешностей мал, но все они смещены относительно нуля на большую величину bΣ. Можно объединить bΣ и σΣ в один, подсчитав меру рассеивания суммарной погрешности относительно нулевого значения по формуле

σ₀Σ=√ σΣ²+bΣ² (11)

Иногда пользуются другим обобщенным критерием – критерием максимальной погрешности. Понятие максимальной погрешности является статистическим: это не самая большая возможная погрешность, ибо теоретически она может оказаться сколь угодно большой, хотя вероятность такого события тем меньше чем больше эта величина. Максимальная погрешность – значение погрешности, вероятность превышения которой равна заданной малой величины порядка 0,01, 0,001 и тому подобное. Например, при нормальном законе распределения погрешности ∆ вероятность то что погрешность превысит значение ∆m=b+3σ (12) составляет 0.003%, если ∆m≤b+3σ, то 0,997. Очень часто именно эта величина принимается за основу при определении понятий максимальной погрешности. Если известно что закон Р(∆), то максимальной погрешностью считают величину определяемую по формуле 12. Закон распределения суммарной ошибки цифрового преобразования Р(∆) часто принимают аналогичное предположение. Так как в законе распределения погрешности ∆с и ∆у обычно близки к нормальному, а роль составляющей ∆к можно сделать незначительной путем выбора величины кванта ∆х. Если например, σс=σу=σк и при этом выбрано ∆х=2σ, среднеквадратическое суммарной инструментальной погрешности без учета погрешности квантования

σ_и=√σ₀²+σ_у²=1.41σ (13),

а среднеквадратичность полной погрешности преобразования рассчитанная по формуле 9 оказывается равной σΣ=1.53σ. Что лишь на 8.6% превышает суммарную инструментальную. Считая суммарный закон нормальным можно по аналогии с 12 можно записать выражение для максимальной суммарной погрешности

∆m_Σ=b_Σ+3σ_Σ (14)

Все приведенные выше статистические характеристики погрешности относятся к такому режиму АЦП, когда многократно повторяются преобразования случайной величины х, при этом не рассматривается случай когда нужно следить за ходом изменении величины х во времени, то есть за функцией времени х(t). Этот случай типичен для измерительных устройств входящих в систему управлении непрерывными технологическими процессами.