Нечеткие множества в решении экономических задач
В процессе создания моделей баз знаний специалисты сталкиваются с проблемой отражения и использования нечеткой, то есть неопределенной информации.
Представление таких знаний “как высокий человек”, “добросовестный поставщик”, “надежный партнер” и т.д., потребовали нового взгляда на методы их формализации.
Задачи, решаемые человеком, в большинстве случаев опираются именно на нечеткие, размытые и неопределенные знания о процессах или событиях. Знания человека в большинстве случаев нечеткие. Он оперирует такими понятиями как высокий, низкий, горячее, холодное, бедный, богатый и т.д. в повседневной производственной практике и быту.
Нечёткое(или размытое, расплывчатое, туманное, пушистое) множество — понятие, введённое Лотфи Заде в 1965 г. Он расширил классическое понятие множества, допустив, что характеристическая функция (функция принадлежности элемента множеству) может принимать любые значения в интервале [0,1], а не только значения 0 или 1. Для того чтобы такого рода знания можно было использовать для формирования решений, в 1965 году Л.Заде предложил теорию нечетких множеств.
В основе данной теории лежит понятие функции принадлежности, которая указывает степень принадлежности какого-либо элемента некоторому множеству элементов.
Данная функция является субъективной и строится на основании знаний, опыта или ощущений некоторого субъекта к какому-либо объекту, процессу, явлению и т.д.
Степень принадлежности элементов множества Е множеству А можно однозначно представить как:
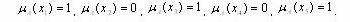
На рисунке иллюстрируется четкая (однозначная) принадлежность элементов одного множества другому.
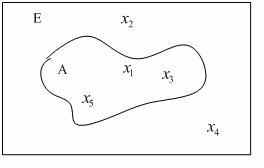
Но принадлежность элементов может характеризоваться и приблизительно, например:
- более или менее принадлежит;
- скореепринадлежит;
- возможно принадлежит и т.д.
Функция принадлежности нечёткого множества — обобщение индикаторной функции классического множества. В нечёткой логике она представляет степень принадлежности каждого члена к данному нечёткому множеству. Степени принадлежности часто смешивают с вероятностями, хотя они принципиально отличны
Для нашего случая функция принадлежности, записывается следующим образом:
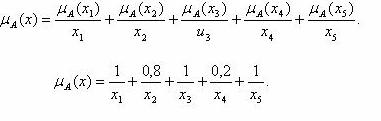
Если функцию принадлежности применить для четких множеств (см. рис. 5.33), то можно получить следующее:
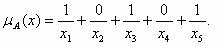
Как правило, функции принадлежности иллюстрируются графически. На рисунке представлено субъективное понимание возраста с помощью функций принадлежности и графиков.
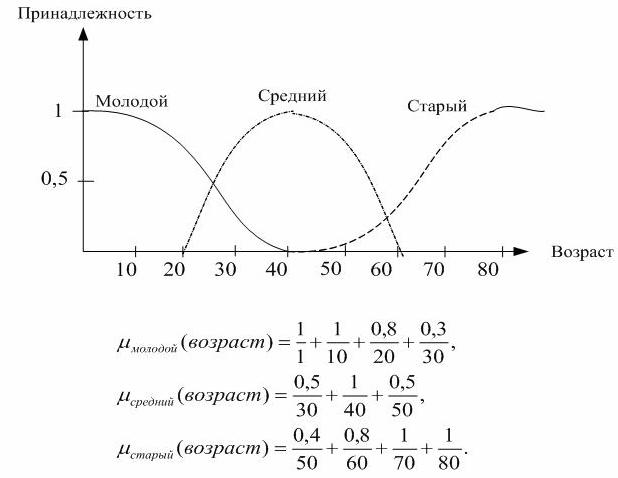
На рис. 5.35 представлено субъективное понимание понятия «низкие процентные ставки».
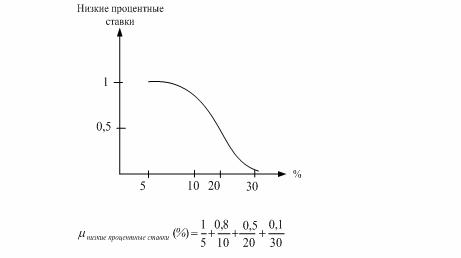
Для того чтобы функцию принадлежности можно было использовать в практических расчетах, вводятся операции пересечения и объединения нечетких множеств.
Операция пересечения нечетких множеств соответствует нахождению минимума значений их функций принадлежности:
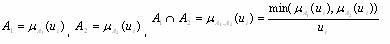
Операция объединения соответствует максимуму значений их функций принадлежности, то есть:
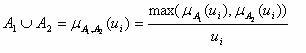 .
.
Дата добавления: 2015-05-21; просмотров: 2291;
