Метод симметричных составляющих
Произвольную несимметричную систему трех векторов А, В, С можно разложить однозначно на три симметричные системы:
– систему векторов прямой последовательности А1; В1; С1;
– систему векторов обратной последовательности А2; В2; С2;
– систему векторов нулевой последовательности А0; В0; С0.
Согласно условию разложения имеем:
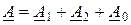 ;
;
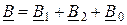 ; (10.1)
; (10.1)
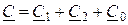 .
.
Для сведения уравнений (10.1) к трем неизвестным вводят оператор фазы а. Модуль оператора фазы равен 1. Таким образом, если любой вектор умножить на а, то модуль вектора не изменится, а лишь произойдет его поворот на 120º против часовой стрелки. Благодаря этому свойству можно векторы каждой из симметричных систем (прямой, обратной, нулевой) выразить через один вектор той же системы, т. е. три неизвестных в уравнении свести к одному.
Оператор фазы а определяется из соотношений:
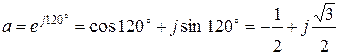 ;
;
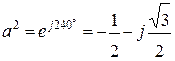 ;
;  .
.
Если принять в качестве основной фазу А, то систему (10.1) при помощи оператора фазы а можно представить в следующем виде:
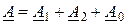 ;
;
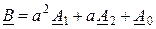 ; (10.2)
; (10.2)
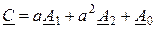 .
.
Совместное решение системы уравнений (10.2) дает:
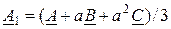 ;
;
 ; (10.3)
; (10.3)
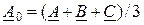 .
.
Степень несимметрии трехфазной системы оценивается коэффициентами несимметрии и неуравновешенности системы.
Абсолютная величина отношения составляющей обратной последовательности к прямой называется коэффициентом несимметрии системы.
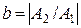 (10.4)
(10.4)
Абсолютная величина отношения составляющей нулевой последовательности к прямой называется коэффициентом неуравновешенности системы.
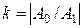 (10.5)
(10.5)
Системы прямой и обратной последовательности являются симметричными и уравновешенными, а система нулевой последовательности является симметричной, но неуравновешенной. Система нулевой последовательности может существовать только в неуравновешенных системах, которые характеризуются следующим условием:  .
.
Геометрическая сумма неуравновешенной системы фазных токов равна утроенному току нулевой последовательности, который протекает в земле или нулевом проводе.
В соответствии с (10.3) по известным несимметричным векторам А, В, С можно найти их симметричные составляющие графическим или аналитическим способами. Пример графического определения симметричных составляющих несимметричной трехфазной системы приведен на рис. 10.1.


Рис. 10.1. Разложение несимметричной системы трех векторов
на симметричные составляющие
10.3. Принцип независимости действия симметричных
составляющих
При несимметричном режиме симметрично выполненной трехфазной цепи все три последовательности можно рассматривать совершенно независимо, так как между отдельными последовательностями нет никакого взаимодействия. Это положение является важным для практического применения метода симметричных составляющих.
Рассмотрим трехфазную цепь (рис. 10.2). Для такой трехфазной цепи справедливы уравнения:

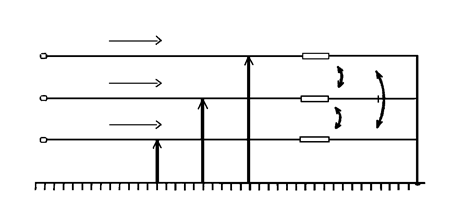
Рис. 10.2. Трехфазная цепь
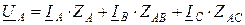 ;
;
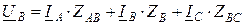 ; (10.6)
; (10.6)
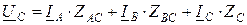 .
.
Положим 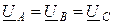 ;
; 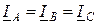 ;
; 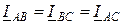 .
.
Используя метод симметричных составляющих к системе токов и напряжений, систему (10.6) с учетом (10.3) можно переписать:
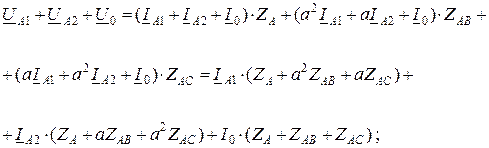
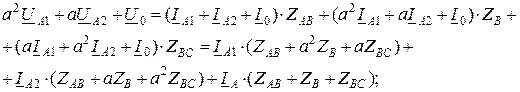
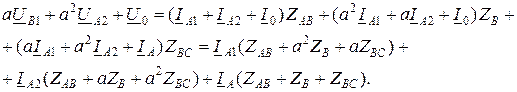
Решение этой систем  ы уравнений относительно симметричных составляющих напряжений дает:
ы уравнений относительно симметричных составляющих напряжений дает:
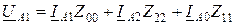 ;
;
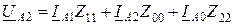 ; (10.7)
; (10.7)
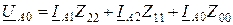 ,
,
где Zii – коэффициенты, составленные из комбинаций сопротивлений исходной схемы.
Уравнения (10.7) устанавливают нарушения принципа независимости действия симметричных составляющих для схемы с неодинаковыми сопротивлениями фаз, для которой протекание токов какой-либо последовательности вызывает падение напряжения всех трех последовательностей.
Элементы электрических систем в нормальных и аварийных режимах по своим физическим параметрам оказываются практически конструктивно симметричными, что позволяет считать:
 ,
, 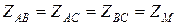 .
.
При этом исходные уравнения значительно упрощаются:
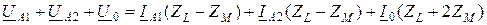 ;
;
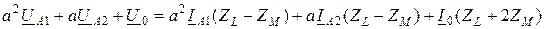 ; (10.8)
; (10.8)
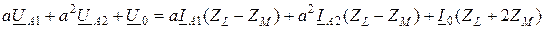 .
.
Решая совместно уравнения (10.8) относительно симметричных составляющих напряжения, имеем:
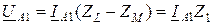 ;
;
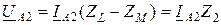 , (10.9)
, (10.9)
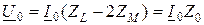 ,
,
где Z0 – сопротивление нулевой последовательности;
Z1 – сопротивление прямой последовательности;
Z2 – сопротивление обратной последовательности.
Уравнения (10.9) отражают принцип независимости действия симметричных составляющих, который состоит в том, что в трехфазной системе с симметричными элементами напряжение любой последовательности может вызвать токи только одноименной последовательности. Точно также токи данной последовательности вызывают в фазах элементов системы падения напряжения только своей последовательности.
ЭДС симметричного трехфазного источника питания образуют симметричную систему векторов прямой последовательности. При нормальной симметричной нагрузке или при трехфазном КЗ такая система ЭДС способна вызвать только токи прямой последовательности, так как напряжения и ЭДС других последовательностей в таких режимах отсутствуют.
При несимметричных КЗ в месте повреждения возникают несимметричные напряжения вследствие нарушения симметрии режима. Вся схема в целом и по частям продолжает оставаться симметричной. Появляющиеся при этом токи обратной и нулевой последовательности вызывают в элементах схемы соответствующие магнитные потоки и падения напряжения.
ЭДС контуров токов обратной и нулевой последовательности можно учитывать падением напряжения в реактивном сопротивлении машины той или иной последовательности подобно тому, как учитывается ЭДС реакции статора машины падением напряжения в соответствующей реактивности. В силу указанных соображений можно считать, что при любом режиме генератор вырабатывает ЭДС только прямой последовательности, а ЭДС обратной и нулевой последовательности генератора равны нулю.
В соответствии с изложенным для произвольного несимметричного КЗ основные уравнения в соответствии со вторым законом Кирхгофа отдельно для каждой последовательности будут иметь вид:
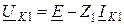 ;
;
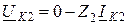 ; (10.10)
; (10.10)
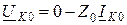 ,
,
где UК1, UК2, UК0, IК1, IК2, IК0 – симметричные составляющие напряжения и тока в месте КЗ;
Е – результирующая ЭДС схемы прямой последовательности относительно точки КЗ;
Z1, Z2, Z0 – результирующие сопротивления схем соответствующих последовательностей относительно точки КЗ.
Уравнения (10.10) содержат шесть неизвестных величин: три составляющие напряжения и три составляющие тока. Недостающие уравнения для определения неизвестных величин получают из граничных условий, которыми характеризуется тот или иной вид несимметричного повреждения.
10.4. Сопротивления различных последовательностей
элементов СЭС
Все сопротивления, которыми характеризуются отдельные элементы в нормальном симметричном режиме, а также в симметричном переходном процессе, по существу, являются сопротивлениями прямой последовательности. Этот термин раньше не вводился, так как в схеме протекали токи лишь прямой последовательности. При отсутствии взаимоиндукции между фазами какого-либо элемента его сопротивления прямой, обратной и нулевой последовательности одинаковы, так как они обусловлены только собственной индуктивностью фазы 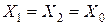 .
.
При наличии магнитной связи между фазами реактивное сопротивление определяется с учетом взаимной индуктивности, которое зависит от того, какая последовательность токов протекает по фазам. Для элемента, магнитосвязанные цепи которого неподвижны друг относительно друга, сопротивления прямой и обратной последовательностей одинаковы, так как от перемены чередования фаз взаимоиндукция между фазами такого элемента не изменяется.
Таким образом для трансформаторов, воздушных и кабельных линий, реакторов  .
.
Сопротивление нулевой последовательности всех элементов резко отличается от сопротивления прямой и обратной последовательностей, так как в этом случае взаимоиндукция сказывается иначе в силу того, что система токов нулевой последовательности совпадает по фазам, в то время как токи прямой и обратной последовательностей по фазам сдвинуты на 120°. Кроме того, на величину реактивности нулевой последовательности сказывается схема соединения фаз рассматриваемого элемента и режим нейтрали. Если нет пути для протекания токов нулевой последовательности, то это равносильно тому, что сопротивление нулевой последовательности равно бесконечности.
10.4.1. Сопротивления обратной и нулевой
последовательности синхронных машин
Реактивное сопротивление обратной последовательности синхронных машин зависит от симметрии ротора. Токи обратной последовательности создают магнитный поток, который вращается относительно статора с синхронной скоростью в обратном направлении вращения ротора и, следовательно, вращается относительно ротора с двойной синхронной скоростью. При своем перемещении этот поток встречает различное сопротивление в расточке статора, поочередно совпадая то с продольной, то с поперечной осью ротора. Если воздушный зазор одинаков по всей окружности расточки машины и ротор симметричен, то в своем перемещении поток обратной последовательности всюду встречает одинаковое сопротивление, как и поток прямой последовательности, в силу чего реактивность обратной последовательности мало отличается от сверхпереходной реактивности.
Значения реактивного сопротивления обратной последовательности приводятся в каталогах и справочниках как параметры машины. При отсутствии таких данных в качестве приближенных значений можно принимать:
– для турбогенераторов и машин с демпферными обмотками  ;
;
– для машин без демпферных обмоток 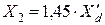 .
.
В практических приближенных расчетах токов, при удаленном КЗ, допускается еще большее упрощение: 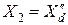 .
.
Реактивность нулевой последовательности. Токи нулевой последовательности синхронных машин создают потоки, одинаковые и совпадающие по времени. Но так как фазные обмотки машины сдвинуты по окружности статора на 120º электрических градусов, потоки нулевой последовательности машины оказываются сдвинутыми в пространстве друг относительно друга на 120º. В силу этого обстоятельства можно считать, что результирующий поток нулевой последовательности синхронных машин определяется потоками рассеяния пазов и лобовых частей.
Реактивность рассеяния будет неодинаковой при протекании токов разных последовательностей. Для токов нулевой последовательности сопротивление рассеяния меньше чем для токов прямой и обратной последовательности, причем это уменьшение зависит от типа обмотки.
10.4.2. Сопротивление обратной последовательности нагрузки
Чтобы установить величину реактивности обратной последовательности обобщенной нагрузки, необходимо сначала оценить величину 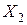 асинхронных двигателей, из которых преимущественно состоит эта нагрузка.
асинхронных двигателей, из которых преимущественно состоит эта нагрузка.
Если в нормальных условиях асинхронный двигатель работает со скольжением s, то по отношению к магнитному потоку обратной последовательности ротор двигателя имеет скольжение 2…5 %. С увеличением скольжения реактивность асинхронного двигателя снижается (благодаря большему проявлению ответной реакции ротора), при этом с достаточной для практических целей точностью можно принимать: 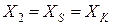 , т. е. реактивность обратной последовательности асинхронного двигателя равна его реактивности короткого замыкания.
, т. е. реактивность обратной последовательности асинхронного двигателя равна его реактивности короткого замыкания.
Таким образом, реактивность обратной последовательности обобщенной нагрузки практически можно принимать такой же, как и для начального момента КЗ, т. е.  OЕ, считая ее отнесенной к полной мощности нагрузки и среднему напряжению той ступени, где она подключена.
OЕ, считая ее отнесенной к полной мощности нагрузки и среднему напряжению той ступени, где она подключена.
10.4.3. Сопротивление нулевой последовательности
реакторов
Реактивность реакторов в основном определяется их самоиндукцией. взаимоиндукция между фазами реактора настолько мала, что практически ею можно пренебречь. По этой причине реактивное сопротивление нулевой последовательности реактора можно считать равным реактивному сопротивлению прямой последовательности, т. е. 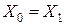 .
.
10.4.4. Сопротивление нулевой последовательности
трансформаторов
Реактивность нулевой последовательности трансформаторов зависит от схемы соединения обмоток и их конструкции.
Прежде всего выясним, в какой мере влияет каждый из этих факторов на величину реактивного сопротивления нулевой последовательности, и лишь после этого обратимся к количественной оценке его величины для трансформаторов.
Если к обмотке, соединенной в треугольник, приложить напряжение нулевой последовательности, то в силу равенства потенциалов каждой из фаз разность потенциалов (напряжения) между любыми фазами равна нулю, следовательно, ток по обмотке, соединенный в треугольник, протекать не будет. К аналогичному выводу можно прийти, если напряжение нулевой последовательности приложено к обмотке, соединенной в звезду без заземленной нейтрали.
Таким образом, сопротивления нулевой последовательности трансформатора со стороны его обмотки, соединенной треугольником ( 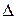 ) или звездой без заземленной нейтрали (Y), всегда равно бесконечности (Х0 = ∞), так как приложенное напряжение нулевой последовательности со стороны указанных обмоток не может вызвать в трансформаторе тока нулевой последовательности независимо от схемы соединения других его обмоток.
) или звездой без заземленной нейтрали (Y), всегда равно бесконечности (Х0 = ∞), так как приложенное напряжение нулевой последовательности со стороны указанных обмоток не может вызвать в трансформаторе тока нулевой последовательности независимо от схемы соединения других его обмоток.
Для группы из трех однофазных трансформаторов ток намагничивания не зависит от того, какая симметричная система напряжения подведена к ней, магнитный поток каждой фазы имеет отдельный магнитопровод. Поэтому в данном случае ток намагничивания нулевой последовательности 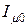 столь же мал, что и ток намагничивания прямой (или обратной) последовательности, что позволяет пренебречь им, т. е. считать
столь же мал, что и ток намагничивания прямой (или обратной) последовательности, что позволяет пренебречь им, т. е. считать 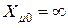 .
.
Это справедливо также для трехфазных четырех- и пятистержневых (броневых) трансформаторов, поскольку при таких конструкциях магнитные потоки нулевой последовательности замыкаются через свободные от обмотки стержни магнитопровода.
Иные условия имеют место в трехфазных трехстержневых трансформаторах. Намагничивающие потоки нулевой последовательности каждого стержня не могут замыкаться по магнитопроводу других стержней, т. к. они заняты потоками от токов своих фаз, что вытесняет их на стенки и крышку бака. В результате значительного увеличения магнитного сопротивления (потоки нулевой последовательности преодолевают магнитное сопротивление воздушного промежутка между ярмом и баком трансформатора) реактивность намагничивания нулевой последовательности существенно уменьшается, продолжая численно оставаться много больше реактивностей рассеяния обмоток трансформатора.
Обратимся к количественной оценке реактивного сопротивления нулевой последовательности трансформаторов.
При соединении обмоток 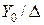 (рис. 10.3 а) ЭДС нулевой последовательности вторичных обмоток будут вызывать соответствующие токи, которые циркулируют только в этих обмотках, не выходя за их пределы. Это позволяет в схеме замещения замкнуть концы вторичной обмотки на нулевой провод. Тогда значение сопротивления
(рис. 10.3 а) ЭДС нулевой последовательности вторичных обмоток будут вызывать соответствующие токи, которые циркулируют только в этих обмотках, не выходя за их пределы. Это позволяет в схеме замещения замкнуть концы вторичной обмотки на нулевой провод. Тогда значение сопротивления 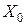 может быть записано так:
может быть записано так:
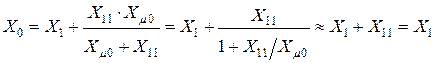 .
.
Имея в виду, что величина 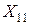 значительно меньше
значительно меньше 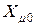 (
( 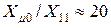 ), можно считать, что и для трехстержневого трансформатора с соединением обмоток
), можно считать, что и для трехстержневого трансформатора с соединением обмоток 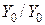 (рис. 10.3 б)
(рис. 10.3 б) 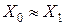 .
.
При соединении обмоток 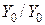 (рис. 10.3 в) сопротивление нулевой последовательности
(рис. 10.3 в) сопротивление нулевой последовательности 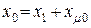 .
.
Для трехфазных групп однофазных трансформаторов или четырех и пятистержневых трансформаторов при соединении обмоток 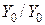 с учетом
с учетом 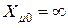 имеем:
имеем: 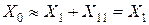 .
.

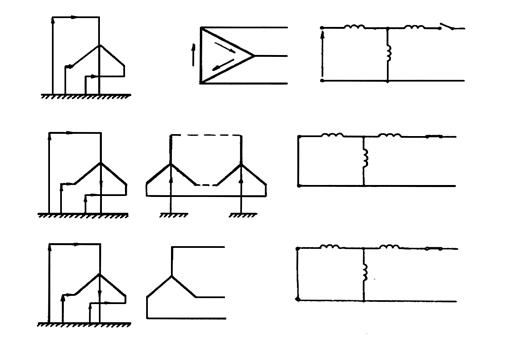
Рис. 10.3. К определению Х0:
а – при соединении обмоток Y0 /Δ;
б – при соединении обмоток Y0 /Y0;
в – при соединении обмоток Y0 /Y

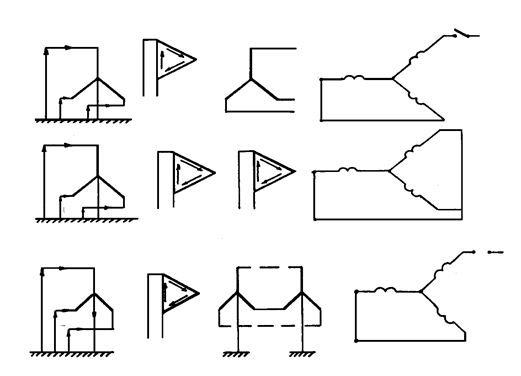
Рис. 10.4. Схемы замещения трехобмоточных трансформаторов
для токов нулевой последовательности
Сопротивления нулевой последовательности для трехобмоточных трансформаторов рассчитываются исходя из групп соединения обмоток.
В варианте «а» (рис. 10.4) ток нулевой последовательности в обмотке III не протекает, следовательно, 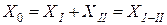 .
.
Если в варианте «б» путь токов нулевой последовательности на стороне III обмотки обеспечен, то в схему нулевой последовательности трансформатор вводится полной схемой замещения.
В варианте «в» ток нулевой последовательности протекает по всем обмоткам трансформатора: 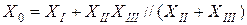 .
.
10.4.5. Сопротивление нулевой последовательности
воздушных ЛЭП
В практических расчетах используют приближенные значения сопротивлений нулевой последовательности, считая, что:
для одноцепных линий без тросов 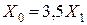 ;
;
для одноцепных линий с тросами 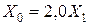 ; (10.11)
; (10.11)
для двухцепных линий без тросов 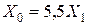 ;
;
для двухцепных линий с тросами 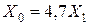 .
.
Таблица 10.1
| Наименование элемента | Трехфазное КЗ | Прямая последовательность | Обратная последовательность | Нулевая последовательность | |
| ИЕ | ОЕ | ||||
| Синхронный генератор | 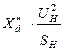
| 
| 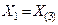
| без ДО
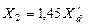 с ДО
с ДО
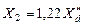
| 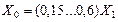
|
| Воздушная ЛЭП | 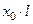
| 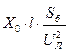
| 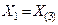
| 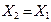
| одноцепная с тросами 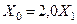 одноцепная без тросов одноцепная без тросов 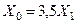 двухцепная с тросами
двухцепная с тросами 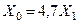 двухцепная без тросов
двухцепная без тросов 
|
| Кабельная ЛЭП | 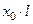
| 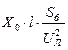
| 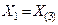
| 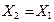
| 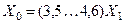 , ,
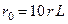
|
| Токо-огранич. реактор | 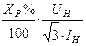
| 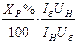
| 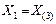
| 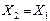
| 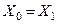
|
Окончание таблицы 10.1
| Наименование элемента | Трехфазное КЗ | Прямая последова-тельность | Обратная последовательность | Нулевая последовательность | |
| ИЕ | ОЕ | ||||
| Асинхронный двигатель | 
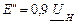
|  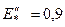
| 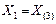
| 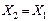
| 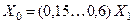
|
| Обобщенная нагрузка | 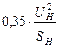
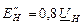
|  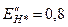
| 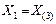
| 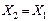
| Определяется элементами |
| Двухобмот. трансформ. | 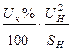
| 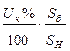
| 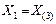
| 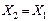
| Определяется соединением обмоток |
| Синхронный двигатель, компенс. |  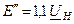
|  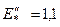
| 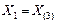
| 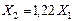 опускается опускается 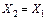
| 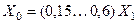
|
10.4.6. Сопротивление нулевой последовательности
кабелей
Токи нулевой последовательности возвращаются по оболочке кабеля и по земле. Оболочка кабеля оказывает такое же влияние, как и трос в воздушных линиях, т. е. увеличивает сопротивление нулевой последовательности. Величины сопротивления нулевой последовательности для кабелей в приближенных расчетах принимаются:
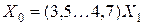 ;
; 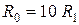 ,
,
где R1 и Х1 – соответственно, активное и индуктивное сопротивления прямой последовательности кабеля.
Формулы для определения сопротивлений прямой, обратной и нулевой последовательностей элементов системы электроснабжения приведены в табл. 10.1.
Дата добавления: 2015-05-19; просмотров: 4993;
