Ток включения трансформатора

Операторный и классический методы решения задач широко применяются во всех случаях, когда системы дифференциальных уравнений переходных процессов являются линейными. Если же хотя бы одно уравнение нелинейно, то такая система уравнений решения в общем виде не имеет. Нелинейные системы дифференциальных уравнений решаются численными методами. В ряде случаев решение нелинейных дифференциальных уравнений можно существенно упростить, применяя графоаналитические методы. В качестве примера такого случая рассмотрим переходный процесс при включении в сеть ненагруженного трансформатора.

При включении первичной обмотки трансформатора на напряжение

,

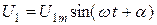при разомкнутой вторичной обмотке переходный процесс описывается дифференциальным уравнением

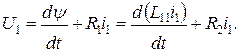(5.25)

При ненасыщенной магнитной цепи коэффициент L₁₁ – постоянная величина и решение уравнения (5.25) имеет вид:

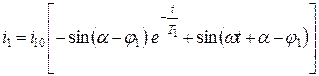, (5.26)

где i₁₀ – амплитуда установившегося тока холостого хода трансформатора;

Т₁ – постоянная времени первичной обмотки трансформатора (при ненасыщенной магнитной цепи);

α – угол включения;

φ₁ – фазный угол тока.

Постоянная времени 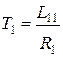,фазный угол тока первичной обмотки

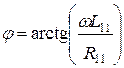.(5.27)

Величина тока первичной обмотки трансформатора при расчете по выражению (5.26) может достичь удвоенного значения установившегося тока холостого хода трансформатора, если включение трансформатора в сеть произошло в момент, когда α = 0.

Однако из практики известно, что ток включения трансформатора может в сотни раз превышать величину установившегося тока холостого хода. Объясняется это влиянием насыщения магнитной цепи.

Следовательно, допущение о ненасыщенности магнитной цепи не отражает действительной картины явления. С изменением насыщения магнитной цепи индуктивность обмотки трансформатора не остается постоянной и коэффициент L₁₁ является нелинейной функцией тока. Поэтому с учетом насыщения магнитной цепи уравнение (5.26) становится нелинейным и решения относительно тока в общем виде не имеет. Однако полное потокосцепление первичной обмотки 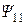является величиной, линейно связанной с напряжением 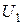. Поэтому кривую тока 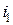с учетом влияния насыщения магнитной цепи можно построить графо-аналитическим методом, используя кривую намагничивания сердечника трансформатора и разрешая уравнение (5.26) относительно потокосцепления 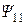. Учитывая, что при разомкнутой вторичной обмотке потокосцепление 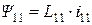, подставляем 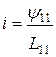в уравнение (5.25), тогда

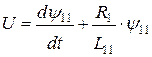. (5.28)

Отношение 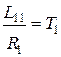изменяется при нарастании тока включения от нуля до максимума в довольно широких пределах. Возможны различные допущения, линеаризующие уравнение (5.26).

Например, допускают, что величина L₁₁остается постоянной, равной среднему значению индуктивности на интервале изменения тока или своему минимальному насыщенному значению. В последнем случае правильно определяется амплитуда тока включения, однако, для остальных моментов времени значения тока получаются несколько завышенными. Насыщенное значение индуктивности первичной обмотки трансформатора можно выразить через ее ненасыщенное значение, исходя из следующего равенства:

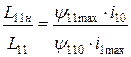. (5.29)

Принимая Т₁ величиной постоянной и заменяя потокосцепление ψ₁₁ через поток ( 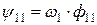), получим линейное дифференциальное уравнение:

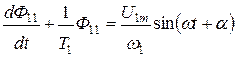. (5.30)

Решение уравнения имеет вид:

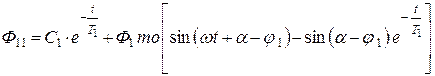, (5.31)

где 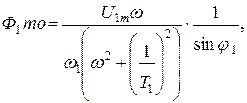а постоянная С₁ определяется из условия, что при t = 0 поток в сердечнике трансформатора Ф₁₁равен остаточному потоку Ф_ост, т. е. С₁ = Ф_ост.

Таким образом,

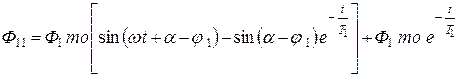, (5.32)

где φ₁ – фазный угол;

Ф₁то – амплитуда установившегося потока холостого хода трансформатора.

Амплитуда тока включения во много раз превышает установившееся значение тока холостого хода. Расчеты показывают, что при Ф₁₁, соответствующем индукции 1,4 Т, отношение амплитуды тока включения к установившемуся значению тока холостого хода достигает 50-80, а при больших индукциях – 100-120. Так как ток холостого хода трансформатора составляет 5-10% от номинального тока, то, очевидно, что ток включения трансформатора может превысить номинальный ток в 6-10 раз.

Свободная составляющая тока Ф₁₁ затухает во времени. Соответственно, уменьшается амплитуда тока включения. Полное затухание тока включения трансформатора средней мощности происходит за 6-8 с, а в мощных трансформаторах продолжается до 20 с.

Наиболее благоприятные условия включения имеют место в момент, когда напряжение сети достигает максимального значения. В этом случае свободная составляющая тока отсутствует, и по магнитопроводу сразу потечет только установившийся поток трансформатора, а по первичной обмотке трансформатора – установившийся ток холостого хода.

Контрольные вопросы

1. Какие основные допущения принимают при анализе переходного процесса в неподвижных магнитосвязанных цепях?

2. При каком условии индуктивности и взаимные индуктивности обмоток трансформатора являются постоянными величинами?

3. Каким образом получается операторная форма записи уравнений переходного процесса трансформаторов?

4. Каков процесс изменения свободных токов двухобмоточного трансформатора?

5. Что такое коэффициент магнитной связи между обмотками и коэффициент рассеяния?

6. Чем обусловлено появление медленно затухающего и быстро затухающего свободных токов?

7. Почему амплитуда тока включения трансформатора во много раз превышает ток холостого хода трансформатора?

6. Переходный процесс в подвижных
магнитосвязанных цепях