Результирующая индуктивность и полное сопротивление двухобмоточного трансформатора в дифференциальной форме

Однофазный двухобмоточный трансформатор представляет собой простейшую цепь с взаимоиндукцией, имеющую всего два индуктивно связанных контура (рис. 5.1). Дифференциальные уравнения для напряжений обмоток трансформатора имеют вид:

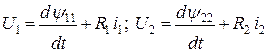, (5.1)

где U₁ и U₂ – напряжения на зажимах первичной и вторичной обмоток;

I₁ и I₂ – токи, протекающие по обмоткам;

R₁ и R₂ – активные сопротивления обмоток.

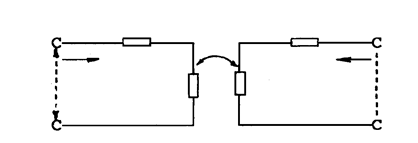
Рис. 5.1. Двухобмоточный трансформатор

Потокосцепления обмоток равны сумме собственных потокосцеплений, создаваемых токами, протекающими по рассматриваемой обмотке, и потокосцеплений взаимоиндукции:

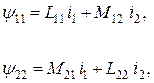(5.2)

где L₁₁ и L₂₂ – полные индуктивности первичной и вторичной обмоток;

М₁₂ = М₂₁ – взаимные индуктивности обмоток, равные друг другу в связи с тем, что обмотки находятся в одинаковых магнитных условиях.

Уравнения для напряжений (5.1) с учетом выражения (5.2) для потокосцеплений обмоток можно записать в виде:

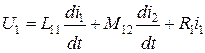, (5.3)

.

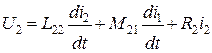В идеализированном трансформаторе принимается, что насыщение магнитной цепи отсутствует, поэтому коэффициенты L₁₁, L₂₂, М₂₁ и М₁₂ – постоянные величины. При таком допущении решение системы уравнений (5.3) не представляет затруднений. Такая картина имеет место, например, при рассмотрении внезапного КЗ трансформатора.

В этом случае при КЗ уравнения (5.3) будут для одной фазы:

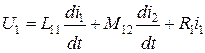; (5.4)

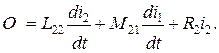
На основе схемы замещения трансформатора, пренебрегая током намагничивания, предположим i₁ = i₂ = i. Сложим уравнения (5.4), получим:

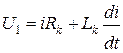, (5.5)

где 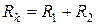; 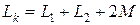– активное сопротивление и индуктивность трансформатора, обусловленная потоками обмоток.

Уравнение (5.5) аналогично уравнению, описывающему переходный процесс в простейшей трёхфазной цепи.

Таким образом, при исследовании процесса КЗ в схеме, содержащей трансформаторы, каждый трансформатор можно рассматривать как обычный элемент электрической цепи со своими сопротивлениями (R_k и L_k) после приведения параметров одной обмотки к другой.

5.3. Уравнения двухобмоточного трансформатора
в операторной форме

Для получения операторной формы записи уравнений, то есть для перехода от функций к изображениям, нужно заменить d /dt на оператор Р. При этом уравнения для напряжений первичной и вторичной обмоток трансформатора будут иметь вид:

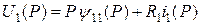, (5.6)

.

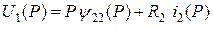В этой системе уравнений

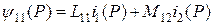, (5.7)

,

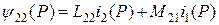где i₁(P) и i₂(P) – изображения токов обмоток;

ψ₁₁(P) и ψ₂₂(P) – изображения потокосцеплений обмоток;

U₁(P) и U₂(P) – изображения напряжений, приложенных к обмоткам.

На практике расчеты ведут в системе относительных единиц, заменяя само- и взаимные индуктивности равными им в системе относительных единиц при базисной частоте индуктивными сопротивлениями. Для обмоток трансформатора

,

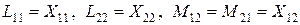где Х₁₁ и Х₂₂ – полные индуктивные сопротивления обмоток трансформатора;

Х₁₂– сопротивление взаимной индуктивности обмоток.

Тогда систему уравнений (5.6) можно представить в следующем виде:

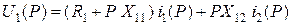, (5.8)

.

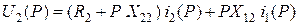Сравнивая комплексные уравнения (5.4) с операторными уравнениями (5.8), приходим к заключению, что уравнения установившегося режима при синусоидальных приложенных напряжениях и постоянных параметрах обмоток могут быть получены из операторных уравнений простой заменой Р на j и изображений функций их комплексными значениями.

5.4. Изменение свободных токов двухобмоточного
трансформатора

Рассмотрим переходный процесс при включении на постоянное напряжение (рис. 5.2) трансформатора. Для простоты будем считать, что все параметры вторичной обмотки приведены к напряжению первичной обмотки.

В том случае, если вторичная обмотка отсутствует или разомкнута, то при включении первичной обмотки на постоянное напряжение в обмотках появятся апериодические составляющие токов, которые будут затухать с постоянными времени, определяемыми только параметрами контуров первичной и вторичной обмоток:

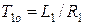, с; 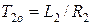, с. (5.9)

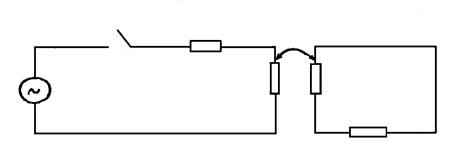
Рис. 5.2. Включение трансформатора на постоянное напряжение

В выражениях (5.9) индекс «о» у постоянной времени указывает, что она определена для данного контура при отсутствии влияния другого контура.

Магнитосвязанные цепи характеризуются коэффициентом связи К и коэффициентом рассеяния С.

Если имеются две магнитосвязанные цепи, то коэффициент рассеяния С представляет собой отношение индуктивности первичной обмотки при замкнутой накоротко вторичной обмотке к индуктивности первичной обмотки при разомкнутой вторичной обмотке, т. е. .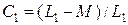

Аналогично для вторичной обмотки .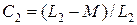

Коэффициент магнитной связи между обмотками .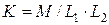

Общий коэффициент рассеяния

.

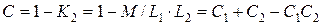При малых С₁ и С₂ можно принять приближенно: С ≈ С₁ + С₂.

В операторной форме при нулевых начальных условиях (U₂= 0) уравнения (5.8) будут иметь вид:

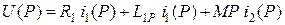, (5.10)

.

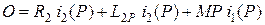Решая совместно систему уравнений (5.10), после промежуточных преобразований имеем:

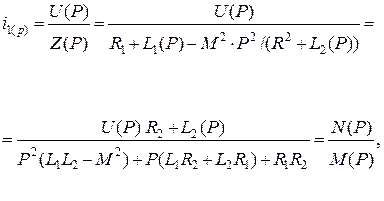(5.11)

где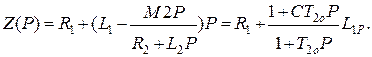

Из уравнения (5.11) видно, что влияние вторичной обмотки приводит к уменьшению L, причем оно тем сильнее, чем меньше рассеяние С.
В пределе, когда С = 1, а, следовательно, К = 0, т. е. при отсутствии магнитной связи между обмотками индуктивность L неизменна.

Найдем корни Р₁и Р₂ характеристического уравнения Z_(P)= 0, предварительно проделав некоторые преобразования.

Так как Т_1о = L₁ / R₁, Т_2о = L₂ / R₂, (L₁ L₂ – M ²) = L₁ L₂ С, то

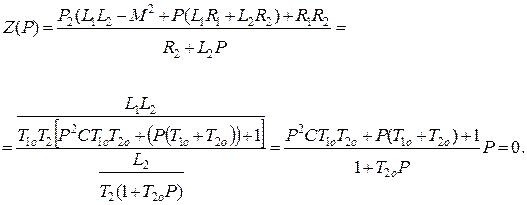(5.12)

Из выражения (5.12) имеем:

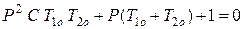. (5.13)

Решение уравнения (5.13) имеет вид:

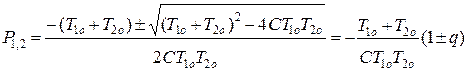, (5.14)

где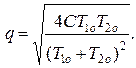

Поскольку всегда (T_1о + T_2о)² > 4СT_1оT_2о, оба корня являются действительными отрицательными числами.

Наличие двух корней свидетельствует о том, что свободный ток в каждой обмотке состоит из двух составляющих, затухающих по экспоненте с постоянными времен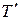и и .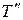

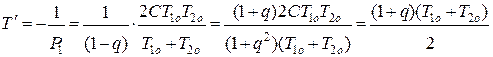(5.15)

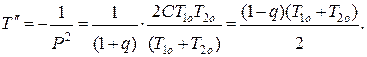
Для , , .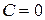

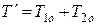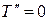Для нахождения тока первичной обмотки в функции времени воспользуемся для выражения (5.11) формулой разложения:

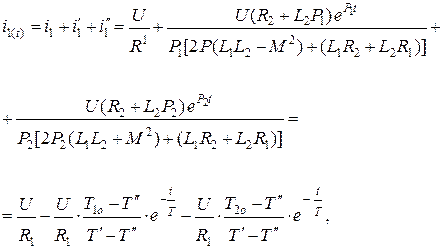(5.16)

где i' – медленно затухающий свободный ток;

i" – быстро затухающий свободный ток.

Аналогично находится ток во вторичной обмотке.

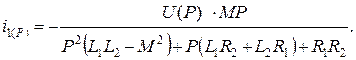(5.17)

Воспользовавшись теоремой разложения, имеем ток вторичной обмотки в функции во времени:

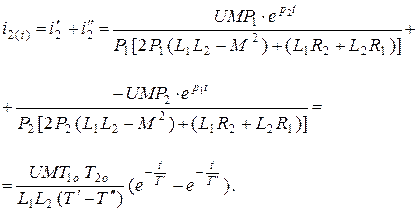(5.18)

Естественно, что при включении на постоянное напряжение принужденный ток во вторичной обмотке отсутствует, а начальные значения свободных токов равны и взаимно противоположны:

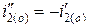. (5.19)

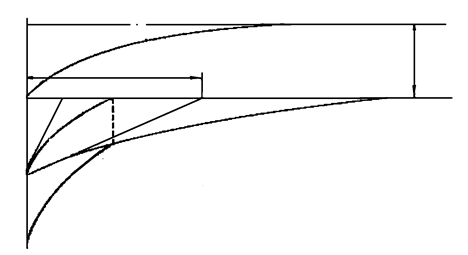
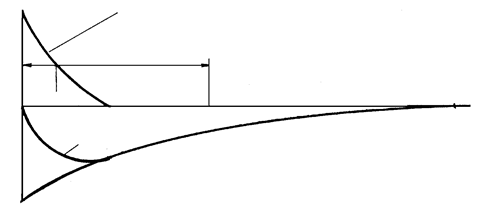
Для рассматриваемого переходного процесса на рис. 5.3 приведены кривые изменения свободных токов и их отдельных составляющих. Начальные значения свободных токов первичной обмотки (рис. 5.3 а) для простоты приняты равными 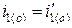. Ток 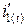,возрастая по экспоненциальному закону, стремится к своему установившемуся значению U/R. Ток i_2(t) вначале возрастает до некоторого своего максимального значения, а затем затухает, стремясь к нулю.

В начальной стадии переходного процесса скорость изменения токов в обмотках велика, что обусловлено наличием быстрозатухающих свободных токов ( 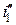и 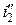). После их полного исчезновения скорость изменения токов резко снижается, так как характер изменения общего тока определяется в этом случае оставшимся медленно затухающим свободным током (для первичной обмотки – 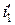, для вторичной – ).

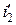Медленно затухающие свободные токи практически связаны с изменением только общего магнитного потока или потока взаимоиндукции между контурами, а быстро затухающие свободные токи – только с изменением потоков рассеяния контуров.

а

б

Рис. 5.3. Кривые изменения токов первичной (а) и вторичной (б) обмоток трансформатора при включении его на постоянное напряжение