Принцип возрастания энтропии.

Принцип возрастания энтропии является обобщающим результатом второго начала термодинамики и вытекающих из него следствий. Второе начало термодинамики устанавливает невозможность передачи теплоты от тел с более низкой температурой телам с более высокой температурой без компенсации, или в другой формулировке – невозможность создания вечного двигателя 2-го рода. Исходя из этого, можно установить, что для любой системы, находящейся в равновесном состоянии или претерпевающей равновесные, т.е. обратимые изменения, существует однозначная функция состояния, называемая энтропией. Энтропия является координатой состояния и в этом смысле определяет количество теплоты при равновесных тепловых взаимодействиях. Для изолированной в тепловом отношении системы тел (адиабатная система) суммарное изменение энтропии 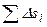всех тел и подсистем, участвующих в любых обратимых процессах, включая изменение энтропии окружающей среды 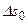(если окружающая среда является частью рассматриваемой изолированной системы), равно нулю. Сказанное можно записать следующим образом:

.

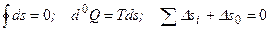Эти уравнения выражают второе начало термодинамики для равновесных систем и обратимых процессов; индекс 0 у знака дифференциала означает, что в общем случае Q (и L) не являются функциями состояния, a d⁰Q и d⁰L – полными дифференциалами.

При любых необратимых процессах в замкнутой адиабатной системе (общая масса не изменяется) энтропия системы возрастает, т.е.

.

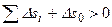Условие внешней тепловой изоляции на контрольной поверхности всей рассматриваемой системы является единственным ограничением. В связи с этим приведенная формулировка принципа возрастания энтропии является более общей по сравнению с формулировкой этого принципа для изолированной системы тел.

Принцип возрастания энтропии определяет направление какого-либо процесса или химической реакции в адиабатной макросистеме. Он отражает возможность или невозможность протекания процессов и определяет условия, необходимые для их осуществления. Принцип возрастания энтропии не является абсолютным: его применимость ограниченна. Например, для микросистем (по размерам сопоставимых с молекулами), для систем в возбужденных состояниях, а также для систем неограниченных размеров этот принцип неприменим.