Системи автоматичного регулюванняз запізнюванням.

Припустимо, що в системі (рис. 2.26) між регулювальним органом і резервуаром значна відстань. Оскільки трубопровід має довжину / і швидкість у руху газу, дістанемо систему з запізнюванням 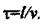Лінійна система з

запізнюванням має одну або кілька запізнілих ланок.

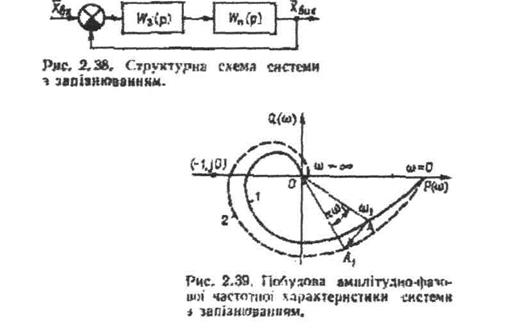
Як правило, запізнювання мають регульовані об'єкти, оскільки елементи системи практично завжди можуть бути підібрані так, щоб виключити запізнення. Структурну схему такої системи звичайно зображують у вигляді послідовно з'єднаних запізнілої ланки і динамічних ланок без запізнювання. Відповідно до рис. 2.38 передаточна функція розімкнутої системи є добутком передаточних функцій ланок:

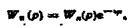(2.1*9)

де 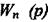- передаточна функція системи без урахування запізнювання;

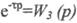- передаточна функція запізнілої ланки.

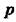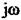Стійкість системи із запізнюванням найпростіше визначити за допомогою критерію Найквіста -- Михайлова, використовуючи вираз (2.119). Замінивши у виразі (2.119) на , дістанемо рівняння амшіітудно-фазової характеристики розімкнутої системи з запізнюванням:

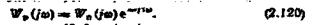
Зобразивши W„ (jo) У показовій формі, дістанемо

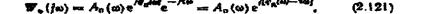
де 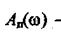- модуль частотної функції системи без урахування запізнення;

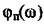- аргумент цієї функції.

Із рівняння (2.121) видно, що амплітудно-фазова характеристика системи з запізнюванням може бути побудована за амплітудно-фазовою характеристикою системи без урахування запізнювання, якщо повернути кожен її радіуовектор за годинниковою стрілкою на кут, який дорівнює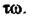

Припустимо, що система без урахування запізнювання має амплітудно-фазову характеристику (рис. 2.39, крива 1). Узявши частоту проведемо радіус-вектор ОА. Визначимо і відкладемо в додатному напрямі кут 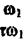. На перетині дуги, утвореної радіусом-вектором ОА, і радіуса-вектора 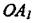дістанемо точку шуканої характеристики, що відповідає частоті 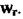Аналогічно можна дістати точки для інших частот, за якими будуємо амшнтудно-фазову характеристику 2 системи з запізнюванням. Система стійка, оскільки амплітудно-фазова характеристика 2 із запізнюванням не охоплює точку з координатами 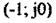на комплексній площині.

Години