Функції алгебри логіки та їх мінімізація.

Алгебра логіки оперує двома числами -Oil, Функціональні елементи автоматичних систем також двопозиційні, наприклад, контакт замкнутий або розімкнутий, через обмотку йде струм або вона знеструмлена і т. д. Якщо один стійкий стан позначити 1, а інший - 0, можна розглядати І і 0 як істинність або помилковість висловлювань. Логічна функція - це залежність величини від однієї або від кількох двійкових змінних, що виражаються через Oil. Сама функція також двійкова.

Звичайно змінні і функції позначають літерами латинського алфавіту. Дужки показують порядок операцій. У системах автоматики застосовують логічні елементи, які реалізують певну логічну функцію.

В алгебрі логіки розрізняють три основні логічні функції (операції): заперечення (інверсія); додавання (диз'юнкція) і множення (кон'юнкція).

Функцію (операцію) заперечення записують як Р=А, Саме заперечення позначають через А і читають «не А». Для операції заперечення справедливі вирази; 0=1 ;1=0; А=А. Стосовно схем автоматики цю операцію називають НЕ, а

пристрій для її реалізації - логічним елементом НЕ. Коли на виході сигналу немає, на виході елемента НЕ встановлюється 1, і навпаки.

Функцію додавання для двох змінних записують у вигляді 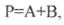її і

логічний елемент позначають АБО. Для операції додавання справедливі співвідношення 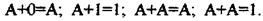На виході логічного елемента

АБО з'являється 1 тільки тоді, коли вона подана на один або на кілька його входів.

Функцію множення для двох змінних можна записати як Р-АВ. Операцію множення і логічний елемент позначають через І. Для цієї операції справедливі вирази Логічний елемент І має кілька входів і один

вихід. На виході 1 з'явиться тільки в тому разі, коли на всі виходи одночасно подано 1.

Із двох логічних змінних можна скласти чотири поєднання: Ці комбінації дають змогу мати 16 елементарних логічних операцій ^логічних функцій), які наведені у табл. 2.4. До таблиці серед усіх функцій входять і три основних - НЕ, АБО, І. Із табл. 2.4 видно, що будь-яку логічну функцію можна зобразити за допомогою системи з трьох основних логічних функцій:

В основу алгебри логіки покладено такі закони:

або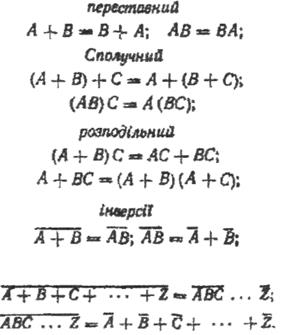

Використовують також операції, що прирівнюються до законів:

Ми пересвідчились, що три основні логічні функції І, АБО, НЕ дають змогу зобразити будь-яку функцію алгебри логіки. Систему елементарних логічних функцій, з яких може бути утворена будь-яка функція алгебри логіки, називають

функціонально поєною системою. Неважко пересвідчитися, що функціонально повними системами також будуть А, А+В; А, АВ; 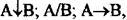В=0; В=А, В=1.

3.4. Елементарні логічні функції

Найголовнішим завданням при розробці систем автоматики є спрощення функціональних залежностей, заданих аналітичне, таблично або за допомогою спеціальних карт. Спрощення виду логічної функції, що реалізується найменшою кількістю простих логічних елементів, називають мінімізацією. Розроблено багато методів мінімізації послідовних і комбінаційних логічних функцій. Розглянемо найпростіший метод безпосереднього спрощення логічної функції.

Вихідну функцію тотожно перетворюють, використовуючи положення і закони алгебри логіки, з метою спрощення. Перетворення треба робити доти, коли функцію спростити вже неможливо. Припустимо, добули таку логічну функцію:

Спростимо її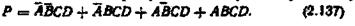

Отже, формула (2.137) еквівалентна (2.138). Формулу (2.138) схемно реалізувати значно простіше, ніж функцію (2.137).