Система астатичного регулювання.

У розглянутій вище системі автоматичного регулювання тиску стиснутого повітря в резервуарі гідравлічний виконавчий механізм з пружиною замінимо виконавчим механізмом двосторонньої дії, а підсилювач типу сопло-заслінка -підсилювачем із золотником (рис. 2.30). Задавальне діяння будемо вводити за допомогою мікрометречного гвинта, який переміщує гільзу підсилювача. Лімб мікрометричного гвинта протарований в одиницях тиску.

При такій заміні кількість елементів у принципіальній схемі і дія системи не змінились. З підвищенням тиску в об'єкті манометрична пружина переміщує важіль і плунжер підсилювача вниз, відкриваючи нижнє вікно гільзи підсилювача. Масло

від джерела надходить у верхню порожнину циліндра виконавчого механізму, і поршень із штоком, перемішуючись униз, зменшує переріз клапана, а отже, й приплив повітря в об'єкт. Плунжер і шток переміщуватимуться до встановлення заданого значення тиску в регульованому об'єкті. При зміні регульованого тиску мікрометричним гвинтом змінюють положення гільзи підсилювача. У цьому разі відкривається одне з вікон гільзи, і масло проходить у нижню або верхню порожнину циліндра, змінюючи переріз клапана до встановлення заданого значення тиску в резервуарі. У структурній схемі системи (рис. 2.29) стануться зміни ~ замість передаточної функції 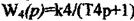і треба вписати передаточну

функцію 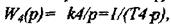оскільки застосований виконавчий механізм є

ідеальною інтегруючою ланкою.

З урахуванням змін передаточна функція розімкнутої системи

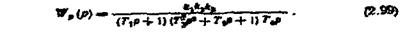
Передаточна функція замкнутої системи

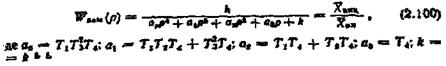
Із виразу (2.100) дістанемо рівняння системи автоматичного регулювання

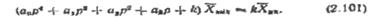
Диференціальне рівняння системи дістанемо, здійснивши зворотний перехід,

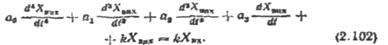
Оскільки в усталеному режимі похідні всіх порядків дорівнюють нулю, із виразу (2.102) дістанемо:

або

У розглянутій системі немає зв'язку між вихідною І вхідною величинами в усталеному режимі, тому на відміну від статичної системи вона називається астатичною. Астатичні системи здійснюють регулювання без статичної помилки при будь-яких сталих збурюючих діяннях.

4. Рівняння динаміки лінійних систем автоматичного регулювання.

Рівняння (2.95) і (2.101) добуті для конкретного випадку статичної й астатичної систем четвертого порядку. Відповідно для лінійної статичної й астатичної систем n-го порядку в загальному вигляді можна

написати рівняння;

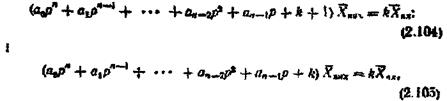
де k - коефіцієнт підсилення розімкнутої системи.

Якщо ліві частини рівнянь (2.104) і (2.105) прирівняти до нуля, дістанемо рівняння, які називаються характеристичними.

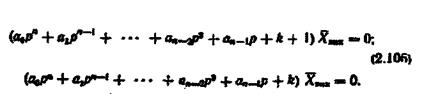
Вони описують поведінку систем автоматичного регулювання в режимі вільних коливань, що характеризується відсутністю будь-яких діянь. Коефіцієнти характеристичного рівняння залежать тільки від значень, окремих параметрів динамічних ланок системи, і при їх сталості вони незмінні. Ці коефіцієнти визначають основні властивості конкретної системи.

Характеристичні рівняння систем звичайно записують у вигляді

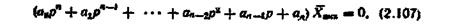
де 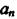— вільний член; 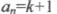- для статичних і 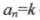-для астатичних систем.

Праві частини рівнянь (2.104) і (2.105) відображують вплив на систему вхідної величини. Як видно з рівнянь, діяння вхідної величини на систему також визначається її параметрами.

Порівнюючи рівняння (2.104) і (2.105), неважко побачити, що в лівій частині рівняння астатичної системи немає вільної одиниці. Ця відмінність мас принципове значення при роботі астатичних систем автоматичного регулювання в усталеному режимі.

4 години