Выбор точки заказа, критический уровень запасов

Выбор точки заказа определяется значением R критического уровня запаса. Заявка на Q единиц товара подается в момент времени t_*, когда текущий уровень запасов i(t) достигнет значения R. Запасы восстанавливаются в момент времени

T_*=t_*+L ,

когда пребывает заказанная партия товара. Здесь величины L - срок поставки товара.

Обозначим 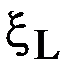величину фактического спроса на промежутке [t_*, T_*]. Идеальное значение величины R равно

R= ,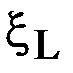

фактическому спросу за время поставки. В этом случае запасы к моменту пополнения становятся равными нулю, и отсутствуют затраты на хранение непотребленной продукции и потери в виде штрафа за отсутствие товара. Значение R интерпретируется как ожидаемый планируемый спрос за время поставки товара.

Для детерминированной модели спроса с известной интенсивностью l величина критического уровня определяется по формуле:

R= 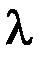L. (2.4)

При случайном характере спроса его фактическое значение 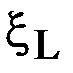в момент принятия решения о пополнении запасов неизвестно. Поэтому при любом выборе значения R возможны ошибки двух родов.

Если спрос окажется больше, чем предсказывалось, т.е. выполнено неравенство

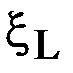> R,

то могут возникнуть потери вследствие неудовлетворенного спроса. Такой потерей может быть, например, потеря прибыли ввиду не продажи товара. Если спрос оказывается меньшим, чем предполагалось,

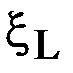< R

то к моменту поступления очередной партии остаются нереализованные остатки.

Примем здесь, что потери от наличия нереализованных остатков менее существенны, чем от неудовлетворенного спроса. Управление запасами должно обеспечить наличие товара на весь период пополнения, отсутствие товара исключается. В этом случае примем критический уровень, равным максимальному значению спроса за время поставки

R= .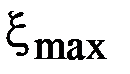

Более точное решение дается в вероятностных терминах. Зададимся малой величиной 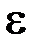=0.01 вероятности неудовлетворенного спроса. Это означает, что выполняется неравенство

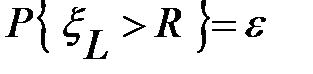
или равносильное ему выражение

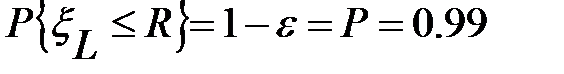
Последнее выражение означает, что критический уровень R находится, как корень уравнения

F(x)=P , (2.5)

где F(x) - функция распределения спроса.

Решение уравнения (2.5) в теории вероятностей называют Р-й квантилью. Таким образом, чтобы исключить отсутствие запасов, критический уровень должен выбираться как Р-я квантиль закона распределения спроса на периоде поставки. Вероятность Р должна выбираться близкой к единице. Например, если спрос за время поставки является нормальной случайной величиной с параметрами (m, ), критический уровень можно определить по правилу "трех сигма"

R=m+3 .