Дискретное преобразование Хартли

Покажем, что функции 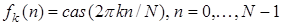, когда 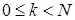обладают свойством ортогональности. Действительно, положим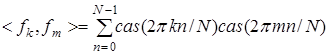 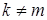. Воспользуемся обозначением 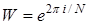. В этих обозначениях 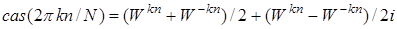. = . 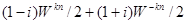Нетрудно видеть, что матрица перехода от одного базиса к другому является унитарной. Отсюда вытекает ортогональность нового базиса.

Преобразование Хартли используется для вычисления спектра, который аналогичен спектру Фурье. Недостаток заключается в отсутствии простой зависимости преобразования от сдвига.