Лекция 20. Строение матрицы Адамара

Элементы матрицы 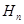можно вычислить непосредственно. Нумерацию строк и столбцов начнем с 0. В этом случае номер строки или столбца задается двоичным вектором: 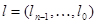. Положим .

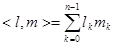Предложение. Элемент матрицы .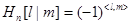

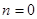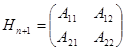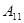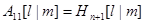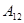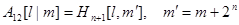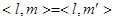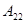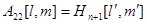Доказательство. Для утверждение очевидно. Рассмотрим , где каждый блок есть матрица Адамара меньшего порядка. Если элемент находится в блоке , то и по предположению индукции формула верна. Если элемент находится в блоке , то . Однако . Если же элемент находится в блоке , то и .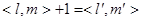

Данное предложение позволяет при работе с матрицами высокого порядка генерировать элементы матрицы, а не хранить их в памяти.