Использование БПФ

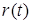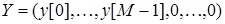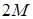Даже при наличии мощного процессора непосредственный подсчет всех нужных значений является трудоемкой задачей. Для уменьшения числа умножений используется следующий подход. Образец заменяется последовательностью длины . Из входной последовательности образуют последовательности длины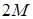 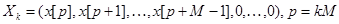, 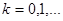. После этого подсчитывается циклическая свертка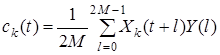

Для отыскания значений свертки используется БПФ. Для этого число 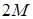должно обладать соответствующими арифметическими свойствами. Покажем теперь, как по найденным значениям 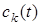подсчитываются значения 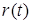. Это проще всего продемонстрировать на примере 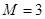. Имеем

,

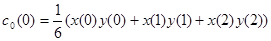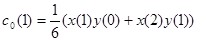
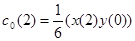. Точно также,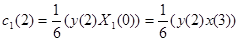

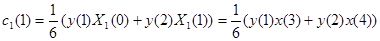. Теперь мы можем найти значения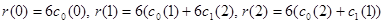

Лекция 18. Эффект Доплера и смежные вопросы

Рассмотрим задачу поиска сигнала заданного вида во входном сигнале на следующем примере. Передатчик излучает сигнал 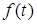, который отражается от объекта и приходит в виде сигнала 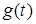. Если объект неподвижен, то

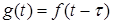. (1)

Здесь 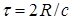, 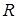- расстояние до объекта, а 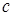- скорость распространения волны. Если же объект движется, то снова имеет место (1), но задержка определяется формулой

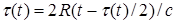(2)

(Сколько времени сигнал движется в прямом направлении столько же и в обратном). Рассмотрим одномерный случай. Пусть объект движется со скоростью 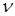и находился в начальный момент на расстоянии 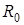. Согласно (2) имеем 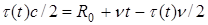. Отсюда

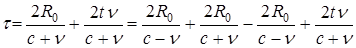
Введем обозначения: 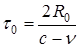. Тогда 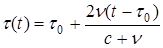. Подставляя в (1) , получим

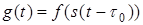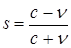, ,(3)

Определение скорости объекта и расстояния до него сводится к отысканию максимума функции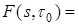

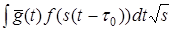. (Множитель 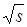добавлен для того, чтобы длина 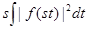на зависела от параметра.

Рассмотрим частный случай, когда 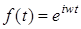. Имеем

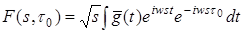. Имеем приближение 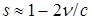. Это позволяет определить скорость по сдвигу частот. Задержка при этом сводится к сдвигу фазы сигнала. Эффект возникает, когда скорость объекта соизмерима со скоростью волны, либо за счет увеличения частоты базового сигнала. Для определения расстояния используют сигнал 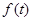в виде одиночного импульса. Здесь имеем снова аналог Wavelet преобразования