Көпфакторлы экстремалды экспериментті оңтайлы жоспарлау
Экспериментті жоспарлау дегенде, бұл жерде, ең алдымен, сөздің жалпы мағынасындағы, эксперименттің қандай да бір кезеңін орындауды қарастыратын ұйымдастыру операцияларын жоспарлау емес, ал түрлі басқарылатын үдерістердің математикалық үлгілерін құру және зерттеуді орындауға қажетті еңбек, уақыт, қаржы шығынын азайту кезінде факторлардың қызметі нұсқаларын оңтайландыру әдісін қарастыру түсіндіріледі.
Белгілі бір жоспар бойынша зерттелетін барлық факторлардың өзара әрекетін ескере отырып, өзгеруін қарастыратын эксперименттің математикалық теориясы – бұл оңтайлы шешім алу мақсатында ЭЕМ мен бағдарламалық қамсыздандыруды қолданумен зерттеуге сапалы жаңа көзқарас.
Зерттеудің мұндай әдісі нәтиженің жоғары нақтылығын, сынақ көлемінің азаюын негіздейді. Әдетте, зерттеу үдерісінің үлгісі коэффициенттері арнайы әдістемемен анықталатын регрессия теңдеуімен, ал олардың оңтайлы шешімі градиентті және градиентсіз әдістермен, мәселен, тік көтерілу жолымен, симплекс әдісімен т.б. сипатталады.
Төменде экспериментті факторлы жоспарлаудың негізгі анықтамасы, мәні мен міндеттері; толық факторлы және бөлшекті факторлы эксперимент көмегімен зерттеу үдерісінің үлгісін құру тәртібі; фактордың сызықты емес шаршы типі есебімен үлгі құру ерекшеліктері; тік көтерілу әдісімен эксперимент жүргізу; экспериментті деректерді есептеу және бағалауға арналған бірқатар формулалар қарастырылады.
Экстремалды міндеттерді шешу бірнеше кезеңде жүзеге асырылады:
1. Ең алдымен, зерттеу нысанын алдын ала зерттеу, зерттеу барысында факторларды априорлы іріктеу жүргізіледі, немесе оны әдеби тілде басқаша «психологиялық эксперимент» деп атайды,сондай-ақ эксперименттер сериясы қойылады, олардың нәтижелерін өңдегеннен кейін факторлардың оңтайландыру параметріне (параметрлеріне) әсерінің дәрежесі туралы болжалды түсінік алынады. Осы зерттеу нәтижесі болып факторлар жігін зерттеу және кейбір аз маңызды факторларды есептен шығару табылады.
2. Келесі кезең – оптимум аймағындағы қозғалыс. Бұл жерде алдымен, аз көлемді сынақтың көмегімен одан арғы экспериментті жүргізетін дұрыс бағыт табылады. Ең қысқа жолмен жүру арқылы оптимум аймағы табылады. Бұл эксперименттер нәтижесі бірінші реттегі регрессия теңдеуімен беріледі.
3. Келесі кезең – алдында табылған оптимум аймағын математикалық (графикалық) сипаттау. Бұл кезең барысында отклик бетін (фнукциясын) сипаттауға арналған сынақтар сериясы, әдетте, екінші реттегі полином қойылады.
4. Алдында айтылғандай, зерттеу «диалогтық» режимде жүргізіледі - зерттеудің әр кезеңін өткізгеннен кейін оның нәтижесіне байланысты экспериментарлы зерттеудің жаңа «стратегиясы» таңдалады, осыған орай, ір кезең сайын эксперимент нәтижелерін мұқият аналитикалық өңдеу жұмысы жүргізіледі.
5. Бірінші немесе екінші реттегі регрессия теңдеуімен ұсынылған математикалық үлгіні алғаннан кейін зерттеу нысанындағы факторлардың сәйкестігінің оңтайлы нұсқасын алу мақсатында, таңдалған ыактор бойынша зерттеу нысанының оңтайлы қызметінің режимін табу мақсатында экстремумға талдау жасалады.
Барлығын рет-ретімен қарастырайық. Мәселен, соқа жұмысын зерттейік. Соқаның күшті көрсеткішін сипаттайтын бастапқы параметр ретінде оның бір сызықты бірліктергі, мәселен, метр қармауышының енінен тартылыс кедергісін Ү қабылдайық. Соқаның тартылыс кедергісіне әсер ететін бастапқы шама ретінде: жер жырту тереңдігін х1; үлесті кедергі коэффициентімен сипатталып, ұсынылатын топырақтың қасиеті мен жағдайын х2; агрегат қозғалысының тереңдігін х3; соқа салмағын х4; агрегат қозғалысының бірдейлігін х5; жел бағыты мен жылдамдығын х6; түрен ұшының қалыңдығын х7 таңдаймыз.
х1, х2, х3, х4, х5, х6, х7 бастапқы шамалар фактор деп аталады. Ү бастапқы шамасы (соқаның оның қармауышы енінің бір бірлігіне тартылыс кедергісі) шешілетін міндет мақсаты мен шартына байланысты мақсат функциясы, отклик, отклик функциясы, оңтайландыру параметрі деп аталады.
Сөйтіп, факторлардың белгісіз функциясы К болып табылатын бастапқы шаманы Ү анықтау керек, басқаша айтқанда, х1 факторының К бойынша соқаның кедергісі үдерісінің қызметінің заңын анықтау керек:

Факторлардың қол жетімді мәндерінің аймағы анықтау аймағы немесе қызмет кеңістігі деп аталады да, W-мен белгіленеді. Х1 және х2 факторлары бойынша анықтау аймағы Wекіфакторлы кеңістік деп, үш фактор бойынша анықтау аймағы үшфакторлы кеңістік деп т.с.с. аталады, ал эксперимент екі-, үш- және т.б. факторлы эксперимент деп аталады. Отклик функциясына факторлар әсері заңдылығын анықтау жөніндегі эксперимент интерполяционды немесе регрессиялы деп аталады.
Wі эксперименттің әр і саласы бойынша төрт (Wі саласы шыңының саны бойынша) сынақ жүргізіледі және олардың әрқайсысы тек екі мән қабылдайды, оларды шартты түрде 0 және 1 немесе -1 және +1 деп белгілейді. Факторлардың бұндай мәндері фактор деңгейлері деп аталады.
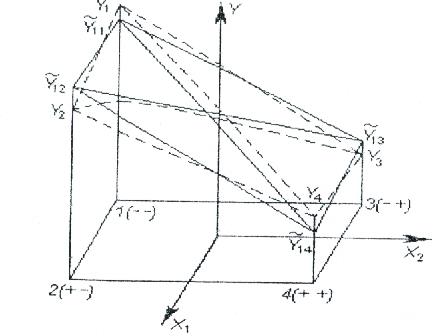
Х2 абсцисса және х1 аппликата бойынша (сурет 4.3) факторлардың төменгі (-1) және жоғарғы (+1) деңгейлері берілген. Х1 және х2 факторларының х1 0 х2 кеңістігіндегі мәні екі деңгейде де нүктемен белгіленген: 1.1; 1.2; 1.3 және 1.4. екі фактордың екі деңгейде сәйкес келуі сынақ санын анықтайды, N=nk, мұндағы n – деңгей саны; k – фактор саны. Біздің мысалда N=nk=22=4. Факторлардың әр деңгейде олардың түрлернуімен сәйкес келетін әр сынақ Ү отклигінің бір мәнін анықтайды, нәтижесінде Ү1 мәнінің саны анықталады. Біздің мысалда Ү11, Ү12, Ү13, Ү14 нүктелерімен шектелген фигура бет түрінде беріліп, отклик беті деп аталады. Үшфакторлы (х1; х2; х3) экспериментті жүргізу кезінде w анықтау саласы параллелепипед немесе текше түрінде беріледі, оның биіктігі N=23=8-ге тең, ал k – факторлы эксперимент кезінде w анықтау саласы гипертекше түрінде болып, N=2k биіктігін көрсетеді, олардың әрқайсысы Үотклик мәнін анықтау бойынша 1 тәжірибені жүргізу қажеттілігіне негізделеді.
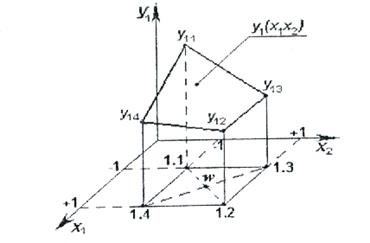
Сурет 4.3 – Екіфакторлы эксперимент «сызбасы және y=f(x1x2) отклик функциясы
Эксперимент міндетіне байланысты N=2k тәжірибесі үнемі жүргізіле бермейді, бұл кезде факторлар екі деңгейде емес, үш деңгейде түрленеді.
Жоспарлау факторларды таңдау, олардың отклик функциясына әсерін анықтау, басқарылатын және басқарылмайтын факторларды анықтау, тәуелді және тәуелсіз факторларды шектеу, аппаратураның нақтылығын анықтау және таңдау жұмыстарынан тұрады.
Таңдалған, іріктелген, сұрыпталғаннан кейін қалған факторлар отклик өлшемінің нақтылығынан жоғары нақтылықпен өлшенетін болуы керек. Факторлар сәйкес келетін және тәуелсіз шамалар болуы керек.
Сәйкес келетін факторлар дегенде барлық жоспарланған факторлар комбинациясының қауіпсіздігімен іске асырылымдылығы (электронды аппаратураны зерттеу кезінде ток пен кедергі шамалары таратылатын қуат пен элемент температурасы шекті шамадан аспайтындай шамада болуы керек), ал тәуелсіз фактор дегенде факторды басқа факторлардың деңгейіне тәуелсіз кез келген деңгейге қою мүмкіндігі түсініледі. Өзара тәуелділік кезінде осы 2 факторды үйлестіретін басқа фактор таңдалуы керек.
Әрбір эксперимент үшін факторлардың түрлену аралығы таңдалады. Түрлену аралығы- экспериментатормен таңдалған факторлардың жоғарғы және төменгі мағыналарының арасындағы айырмашылықтың жартысы.
Сараптау саласының орталығында фактордың мағынасы оны түрлендірудің негізгі деңгейі болып аталады және негізгі индекспен белгіленеді, мысалы, «х1» мәтін астылық индекспен «0» (х1.0.;х2.0;....).
Түрлендіру деңгейінің санын және олардың шекараларын орналастыру кезінде қандай да бір қатаң ұсыныстар мен шектеуліктер жоқ, бірақ та, келесі ережелерге сүйену керек: физикалық факторды түрлендіру аралығы оның мәні тәртіп бойынша эксперименттік қондырғының және оның өлшемінің кемшіліктерінен асып түсу керек; эксперименттің кез-келген саласының басы W факторларды анықтау саласының Ώ ішінде болу керек; аппроксимириялық функциялар ізделетін тәуелділіктен аса қатты ерекшеленбеу керек, (математикалық үлгінің баламалығының талабы); тәжірибеден тәжірибеге ауысар кезде дыбыс мағынасының өзгеруі, ол ең аз дегенде тәжірибе кемшілігінен 2...3 есе жоғары болу керек.
Жоспарлау үрдісінде әдетте факторлардың кодталған мәндері қолданылады, олар жолдың символдармен белгіленеді. Факторлардың физикалық мәндері үлкен символдармен белгіленеді Х1;Х2.....
Кодталған х1 және факторлардың физикалық мәндері Х1 өзара келесі түрде байланысады:

мұнда:  - фактордың түрлену аралығы;
- фактордың түрлену аралығы;
хіж; хіт- J- фактордың төменгі және жоғарғы деңгейлеріне сәйкес;
кодталған факторлар көлеммен нормаланған, экспериментте -1;0;+1 (үш деңгейлі түрленуде) мағынасын қолданатын мөлшерсіз болып табылады.
Дыбыс беру функциясының геометриялық образы (4.1.) факторлық кеңістіктегі дыбыс берудің жоғарғы қабаты деп аталады, ол келесі түрлі бірінші ретті полиноммен жуықталады:
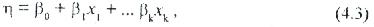
Немесе келеі түрлі екінші ретті полиноммен жуықталады:
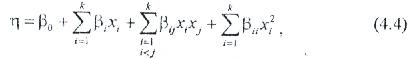
Бұл жағдайда эксперименттің мақсаты регрессия b0; bі; bі?; bii коэффициенттері есептелетін мәліметтерді алу болып табылады және бұл жағдайда теңестіру келесі түрде болады:
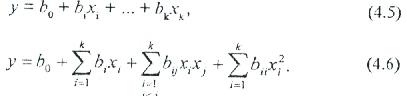
мұнда-У- 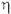 арналған таңдамалы баға;
арналған таңдамалы баға;
Толық факторлы эксперимент- фактор деңгейлерінің барлық мүмкін комбинациялары өткізілетін эксперимент.
Егер К фактор болса, мысалы, үш екі деңгейге түрленсе, онда тәжірибенің барлық мүмкін нұсқаларының саны N2=2к=23=8,
Егер үш деңгейде болса, онда N3=3к=33=27.
Ереже бойынша экспериментті жоспарлау кезінде фактордың төменгі шекарасын -1 белгісімен, ал жоғарысын+1 белгісімен белгілеу шартты түрде қабылданды.
Екі факторлы экспериментте толық факторлы эксперименттің барлық комбинациялары квадрат ұштарымен графикалық түрде ұсынылады (4.4. сурет).
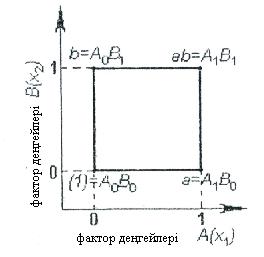
4.4. сурет
А және В факторлары немесе х1с және х2 төменгі деңгейде (1)= А0В0 немесе кіші әріптермен (1)=а0b0. Бұл жағдайларда символдар астында (1) төменгі деңгейде екі факторлы тәжірибеде дыбыс беру мағынасы беріледі.
В факторды жоғарғыда, ал А факторды төменгі деңгейде түрлендіру тәжірибесінде жоспарда А0В немесе а0b=в символдарымен белгіленеді; А жоғарғы, В төменгі деңгейде белгіленсе а= А1В0 немесе а1b0=а, және соңында, А және В жоғарғы деңгейде орналасса аb= А1В1 немесе аb=а1b1 (4.4. сурет).
Толық факторлық эксперименттің тәжірибесінің барлық нұсқалары матрица түрінде ұсынуға болады (4.3. кесте).
4.3. кесте. Екі факторлы экспериментті жоспарлау матрицасы
| Тәжірибе | факторлар деңгейі және олардың өзара әрекеттесуі | Жолдардың кодтық белгілері | Жауап беру | ||||
| А (х1) | В (х2) | АВ (х1х2) | Ү14 | Ү24 | Ү14 | ||
| - | - | + | (1) | Ү11 | Ү21 | Ү?1 | |
| + | - | - | а | Ү12 | Ү22 | Ү?2 | |
| - | + | - | b | Ү13 | Ү23 | Ү?3 | |
| + | + | + | аb | Ү14 | Ү24 | Ү?4 |
Арнайы жоспарлаудың бірінде фактор көздері латынның бас әрпімен АВС және т.б., ал келесіде х1; х2 х3 және т.б.ж белгіленуіне байланысты осы оқулықта екі символда қолданылған- біреуі жақша ішінде, ары қарай ол жойылады.
Бірінші графада тәжірибелер номерлері көрсетілген (қайталанусыз).
Екінші және үшінші графаларда екі фактордың барлық деңгейлердегі барлық нұсқалары көрсетілген. Төртінші графа екі фактордың өзара байланысы кезінде тәжірибелер нұсқасынан қалыптасады, ол көбейту жолымен АхВ алынады. Бесінші графада жолдардың кодтары берілген. Алтыншы, жетінші және қалған графаларда нұсқа және жоғарғы қабаттар бойынша жазылады.
Егер әрбір тәжірибе (жол) бір қайталамада жүргізілсе, онда тек қана бір графа ғана толтырылады (Ү11; Ү12; Ү13; Ү14). Екінші қайталама кезінде дыбыс беру Ү21;Ү22;Ү23;Ү24 және т.б. болып белгіленеді.
АВ (х1х2) факторлардың өзара байланысы екі фактордың бірдей деңгейге өзгерісі дыбыс берудің пропорционалды емес өзгерісімен сүйемелденетіні кезінде байқалады. Мысалы, суглинокты және құмдақ топырақтардың дымқылдығының бірдей өзгерісі кезінде топырақ өңдеуші жұмыс құралдарының топырақты қабуы да бірдей өзгереді.
А,В,С үш тәуелсіз фактормен толық факторлы эксперимент жоспарын құру үшін үш фактордан барлық мүмкін болатын әр комбинация 2 деңгейде (±1) түрленетін комбинацияларды (тәжірибелерді) құру керек. Бұл 23 типті эксперимент жоспары болады.
Бұл эксперимент моделін графикалық түрде үш факторлы кеңістік – текше түрінде беруге болады. Олардың әр басы сынақ нұсқаларының бірін білдіреді, ал ондай нұсқа саны сегіз (4.5 а сурет).
Сынақтың әр нұсқасының кіші латын әрпімен берілген кодтық мәні бар, нұсқалар әртүрлі, мәселен, авс жазуы А, В, және С факторы жоғары деңгейде болатын тәжірибені (эксперимент нұсқасын) білдіреді, вс – А факторлы төмен деңгейде, а – В және С жоғары деңгейде. а, в, с бір әріп жазбалары сәйкесінше А, В, және жоғары деңгейде, қалған екеуі төменгі деңгейде болатын факторды білдіреді. Мұндай эксперимент жоспарын матрица түрінде беруге болады (4.4 кесте).
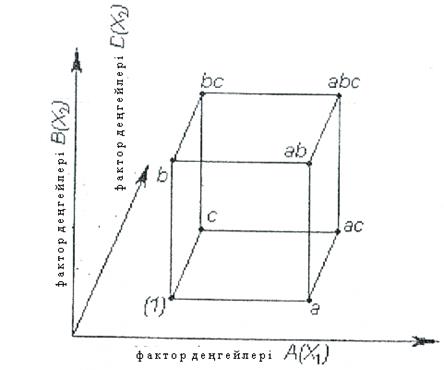
4.5 а сурет 23 типті үшфакторлы эксперимент үлгісінің графикалық бейнесі
Кесте 4.4 – Үшфакторлы экспериментті жоспарлау матрицасы
| Сынақ № | Факторлар деңгейі және олардың өзара әсері | Жолдың кодтық белгісі | ||||||
| А (х1) | В (х2) | С (х3) | АВ (х1х2) | АС (х1х3) | ВС (х2х3) | АВС (х1х2х3) | ||
| - | - | - | + | + | + | - | (1) | |
| + | - | - | - | - | + | + | а | |
| - | + | - | - | + | - | + | в | |
| + | + | - | + | - | - | - | ав | |
| - | - | + | + | - | - | + | с | |
| + | - | + | - | + | - | - | ас | |
| - | + | + | - | - | + | - | вс | |
| + | + | + | + | + | + | + | авс |
Бұл жоспар екіфакторлыдан төртінші бағанға үшінші фактор деңгейінің нұсқасының орналасуымен ерекшеленеді, ал бұл өз кезегінде екі қос өзара әсерді (6 және 7 баған) және бір АВС үштіктің өзара әсерін (8 баған) талап етті. 9 бағанда кодтық белгілер көмегімен сынақтың барлық сегіз нұсқасы берілген: (1), а, в, ав, с, ас, вс, авс.
23 типі бойынша толық факторлы эксперимент (ТФЭ) матрицасы келесі жолмен құрылады: алдымен 23 типті ТФЭ матрицасы құрылады (1, 2, 3, 5 бағандар), сосын үшінші фактор (4-баған) жазылады және содан кейңн ол (с) келесі факторлардың (С, АС, ВС; АВС) барлығына көбейтіледі де, 6, 7 және 8 бағанға жазылады. 4.4 кестесін мұқият қарасақ, 1, 2, 3 және 5 бағандары бойынша алғашқы төрт жол (1, 2, 3, 4) С факторының барлық төменгі деңгейі кезінде 22 типті екі факторлы эксперимент матрицасын білдіреді, 4.4 кестенің басқа бағандарында (5, 6, 7, 8 жолдары) 22 матрицасы С факторының барлық жоғары (+) деңгейі кезінде қайталанады.
6, 7, 8 бағандары С факторын сәйкес бағандағы факторға көбейту нәтижесінде пайда болады, мысалы, 6-бағанның бірінші жолына (-С) мен (-А) көбейту кезіндегі нәтиже ретінде (+) қоямыз, екінші жолда (+А) және (-С) көбейту нәтижесінде алынған (-) белгісі жазылады т.с.с.
Факторлардың кез келген саны үшін толық факторлы эксперимент жоспары осыған ұқсас жолмен құрылады. Төрт факторлы эксперимент (А, В, С, Д) жоспарының матрицасы үшфакторлы эксперимент матрицасының екінші ретін қайталануынан тұрады: біріншісі – Д төртінші фактордың төмен деңгейі кезіндегі, екіншісі – жоғары деңгейі кезіндегі қайталау.
Модель коэффициентін анықтау [22] бойынша баяндалады. Регрессия коэффициенттерді матрицалық алгебра әдістерімен есептеу ыңғайлы болуы үшін жалған ауыспалы х0 = +1 енгізіледі. Сонда қарапайым екі факторлы сызық моделінің теңдеуін бағалау (4.5) мына түрде болады:
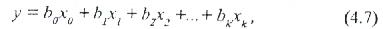
Ал экспериментті жоспарлау матрицасы, мәселен, 22 типі бойынша 4.5 кестеде берілгендей болады.
Кесте 4.5 – х0 = +1 жалған ауыспалымен екі факторлы эксперимент матрицасы
| Сынақ № | Ауыспалылар (факторлар) деңгейі | Отклик Уи | ||
| Х0 | Х1 | Х2 | ||
| + | - | - | У1 | |
| + | + | - | У2 | |
| + | - | + | У3 | |
| + | + | + | У4 |
Фактордың кез келген саны мен (23,24...) эксперимент үшін х0 = +1 жалған ауыспалымен жоспар (матрица) осыған ұқсас жолмен құрылады. b1 коэффициентін анықтаудың түрлі әдістері бар, ең қарапайым түрі – ең аз квадрат әдісі (АКӘ). b1 іздеу үдерісі регрессивті талдау деп аталады. Бұл кезде қағидалы түрде қателіктер жіберіледі, мәселен, барлық тәуелсіз ауыспалы факторлар нақты беріліп, кездейсоқ шама болып табылмайды, ал Уп кездейсоқ шамасы нормалы заңға бағынады, Уп дисперсиясы факторлы кеңістіктің жеке нүктесінде бірдей. Бұл шарттар орындалмайтын үдерістерді зерттеу кезінде АКӘ қолданылмайды, басқа әдістерді қолдану керек [1,28]. Регрессия коэффициентін анықтау келесідей орындалады. Мәселен, нәтижесі 4.6 матрицалық кесте түрінде берілген матрицаға сай эксперимент орындалды. Тапсырма У1, У2, У3, У4 откликтің төрт нүктесі арқылы жазықтық құрудан тұрады. Үш өлшемді кеңістіктегі жазықтықтың орналасуы бір түзуде жатпайтын үш нүктемен анықталатыны белгілі, осыған орай қосымша шарт қажет: ізделіп отырған жазықтықтан нүктелердің ауытқу квадратының саны минимум болуы керек.
4.6. кесте. Екі факторлы зерттеме нәтижелері мен жоспары
| Тәжірибе № | Факторлар деңгейінің мәні | Нәтиже | ||
| Х0 | Х1 | Х2 | Уи | |
| Х01 | Х11 | Х21 | У1 | |
| Х02 | Х12 | Х22 | У2 | |
| Х03 | Х13 | Х23 | У3 | |
Бұл ауытқулар:
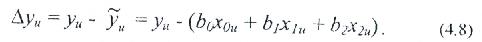
Ауытқулардың саны ▲уи тәжiрибелер немесе жолдардың санына тең (U=1,2,3,4). Қабылданған шарттарға сәйкес b0, b1, b2 коэффициенттерін ▲уи ауытқуы абсолюттік шамасы бойынша аз болатындай етіп таңдау керек.
Регрессия коэффициенттері келесі шарт бойынша анықталса ең төменгі квадраттар тәсіліне сәйкес, ауытқу квадраттары сомасы Σ▲уп ең төмен:

4.6. кестедегі мәліметтерді есепке ала отырып (4.9.) мәні келесідей болады:
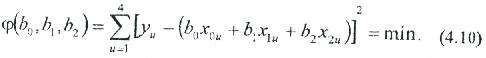
Сондықтан, регрессия коэффициенттерін анықтау тапсырмасы
Демек, регрессия коэффициенттердi анықтаудың есебi функцияның минимумының Ĵ (b) iздеп табуына келесі шарттардың (бiздiң мысалда үш: b0, b1, b2) айнымалыларына апарады:
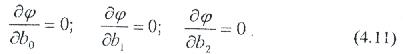
4.6. кесте мәліметтерін қолдана отырып, бұл шарттарды жазуға болады:

Қарапайым түрлену жолымен (4.12) қалыпты теңеу жүйесін алуға болады:
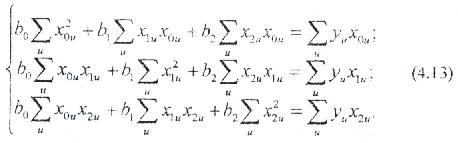
Есептеуіш процедураны жеңілдету үшін сараптаманы жоспарлау үшін анықтағыш нөлден айрықшалануын қарастыру керек (4.13).
Толық факторлы тәжiрибенiң құндылығы тек қана тәжірибе жоспары матрица рототабельдік, симметриялық, нормалау және ортогональность қасиеттерге ие болатындай қалыпта құрылғанда ғана көрінеді.
Ротатабельдік қасиет тең қашықтықтардың жоспардың ортасынан үн қосудың болжалған мәндерiнiң дисперсиясы тұрақты және ең төменгi болғандығында.
Симметрия қасиеті -кез-келген нақты фактор элементтерінің алгебралық сомасы нөлге тең немесе әрбір ауыспалы оң және теріс мәндердің баланс шарттары нөлге тең (4.14):

Нормалау қасиеті кез келген баған элементтерінің квадраты қосындысы түрлі сынақ санына тең болатынымен көрінеді – n жолы:

Ортогоналдылық қасиеті кез келген екі баған элементтерінің жолдық туындысының қосындысы нөлге тең болумен сипатталады:

Мұндағы i және j – баған нөмері немесе фактор нөмері;
и – жол факторларын жинау нұсқасының нөмері;
п – сынақ (матрица жолдарының) нұсқасының жалпы саны.
Осы қасиеттердің және х0и = +1 есебінен (4.13) жүйе теңдеудің сол бөлігінде барлық аралас туынды суммасы нөлге тең, ал фактор квадратының әр суммасы сынақ санына тең (біздің мысалда 4-ке) болатын түрді иеленеді:

Теңдеу жүйесін регрессия коэффициетіне қатысты шешіп, b1 анықтамасы бойынша жалпы теңдеуді аламыз:

Нақты жағдайда екіфакторлы эксперимент мысалы үшін регрессия коэффициенті мынаған тең:
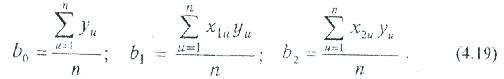
Уи оңтайландыру критерийінің мәні бұл тәуелділіктерде и сынағының қайталануында і орташа мәнін білдіреді.
Жоғарыда факторлардың өзара әрекет әсерінсіз толық факторлы эксперимент мыналы қарастырылды – сызықты үлгі алынды.
Факторлар туындысы типті отклик бетінің (регрессия теңдеуі) сызықсыздығы.
Факторлардың қос өзара әсері орын алатын зерттеу үдерісі сызықсыз үлгімен сипатталады. Факторлардың қос өзара әрекетіне негізделген үлгінің сызықсыздығы факторлар туындысы (бірінші қатар әсері) немесе факторлар квадртаы болып табылатын регрессия теңдеуінің қосымша құрамымен есептеледі.
Факторлардың туындысы типіндегі сызықсыз үлгі төмендегі түрде берілуі мүмкін:
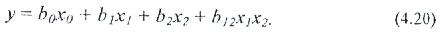
Факторлардың қос өзара әсері бір фактордың у отклигіне (шығыс шамасына) әсері заңдылығы екінші фактордың өзгерісіне тәуелді болғанда орын алады.
Осыған орай, (4.19) сызықсыздығы жағдайында симметрия (4.14), нормалау (4.15) және ортогоналдылық (4.16) шарттарын қанағаттандыратын, х1 және х2 факторларының өзара әсерінің туынды бағаны пайда болуы мүмкін, өзара әсер коэффициентін де (4.18) формуласымен анықтайды. B3 арқылы b12 өзара әсер коэффициентін белгілеп, ал х1х2=х3 болса, (4.20) үлгі мына түрге ие болады:
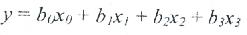
х3 =х1х2 болғандықтан, ауыспалыны түрлендіру деңгейінің мәні х1 және х2 параметрлерін көбейту жолымен алынады (4.7 кесте 7-баған): Сондықтан
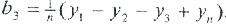
Соқаның тарту кедергісін х1 жер жырту тереңдігі мен х2 топырақтың үлестік кедергісіне байланысты зерттеу кезінде екі фактордың қос өзара әсері есебінен және оны ескермей модель құруға арналған екіфакторлы эксперимент нәтижесі түрінде 4.7 кесте және отклик беті берілген (сурет 4.5)
Кесте 4.7 Соқаны сынау нәтижелері

(4.7) кесте және (4.19) формула деректері бойынша мыналарды аламыз:
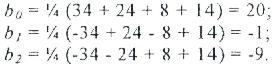
Осыған орай, х1 және х2 факторлардың қос өзара әрекеті есебінсіз регрессияның сызықтық теңдеуі мына түрде болады:
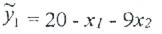
4.5 б суретте 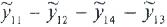 тұтас сызықпен белгіленген.
тұтас сызықпен белгіленген.
Факторлардың қос өзара әсері кезіндегі регрессиясы коэффициенті

B0, b1 және b2 коэффициенттері (4.19) формуласы бойынша есептеледі. Сөйтіп, х1 және х2 факторларының қос өзара әсері есебімен регрессия теңдеуі мына түрде болады:
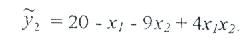
Сурет 4.5,б факторлардың өзара әсері есебімен (үзіксызықты) және есебінсіз (тұтас сызықты) отклик беті
Бұл теңдеу сызықты теңдеуден 4х1х2 құрамымен ерекшеленеді.
4.5 б суретте У1-У2-У3-У4 үзік сызығы бейнеленген – бұл екі фактордың (х1х2 факторларының туындысы сияқты )да бірінші қатарының өзара әсерін ескеретін қисық сызықты бет, отклик беті.
Біздің мысалымызда жыртылған жер тереңдігі факторы мен топырақтың үлесті кедергісі факторының өзара әсері (шындығында – соқаға топырақтың үлесті кедергісі әр тереңдікте әртүрлі).
Үн бетінің сызықсыздығы факторлардың өзара әсерінің басқа типімен сипатталады.
Факторлардың квадртаы типті отклик бетінің (регрессия теңдеуінің) сызықсыздығы.
Бұл жағдайда k факторы бойынша түрленетін үдеріс моделі екінші дәрежелі полиноммен сипатталады.
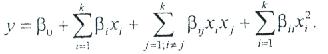
Бұндай полином құру үшін екінші қатар орталығы немесе жоспар ядросы болып 2k ТФЭ таңдалады да, оған факторлы кеңістіктің қосымша (жұлдызды) нүктелері қосылады.
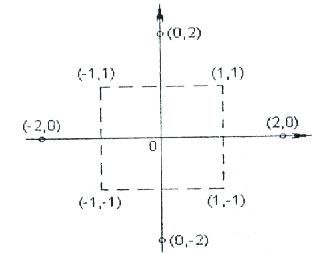
Сурет 4.6. Жұлдызды нүктелер мен 22 ТФЭ нүктелерінің өзара сәйкес орналасуы
Орналасу орны екінші қатарды жоспарлау матрицасының барлық бағандарының ортогоналдылығы шартымен анықталады. Бұндай жоспар екінші қатардың ортогоналды орталық-композициялық жоспары (ООКЖ) деп аталады. Жоспарға ±1 деңгейіне факторлар мәні және х1 = (i=1, 2, 3 … k) координатасының басталу нүктесі енгізіледі және әр координатада х1 = ± а екі жұлдызды нүктесі таңдалады. Бұл жағдайда n=2k+2k+1 қатынасы сынақ нұсқаларының жалпы санын анықтайды. 4.6 суретте а және 0 координаталарымен жұлдызды нүктелер бейнеленген, мұндағы а – жұлдызды иық (плечо) түрленетін факторлар саны жұлдызды нүктелердің орналасуын анықтайды. Факторларының алғашқы дәрежесінің ортогоналдылығы [23] мәні бойынша факторлар квадратының қайта түрленуімен қамтамасыз етіледі.
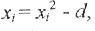
мұндағы: f – факторлар санына тәуелді түзету.
Екіфакторлы эксперимент үшін екінші қатарлы ООКЖ құру мақсатында 4.8 кестесінің [23] деректерін пайдаланамыз.
Кесте 4.8 – Квадратты модульді есептеуге қажет деректер
| Факторлар саны k | Жоспар ядросы | Сынақтың жалпы саны | а жұлдызды иық | d түзету мәні |
| 22 | 1,0000 | 2/3 =0.6667 | ||
| 23 | 1.2154 | 8/15=0.7303 | ||
| 24 | 1.4142 | 4/5=0.80 | ||
| 25-1 | 1.5467 | 4√3/9=0.7698 | ||
| 25 | 1.5960 | 4√86/43=0.8627 |
Кесте 4.9 – Зерттелетін екіфакторлы үдеріс үшін екінші қатардың ортогоналды орталық-композициялық жоспары

Регрессия коэффициенттері төмендегі мән бойынша (жоспардың ортогоналдылығының негізінде) есептеледі.
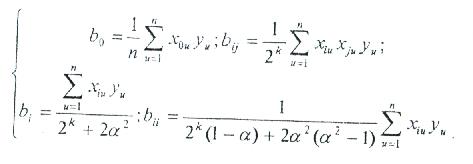
Коэффициенттерді есептеп алып, регрессия теңдеуін жазуға болады.
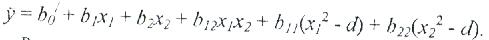
Теңдеу жақшасын ашып, 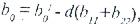 қабылдап, регрессия теңдеуін стандартты формада жазуға болады:
қабылдап, регрессия теңдеуін стандартты формада жазуға болады:
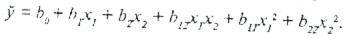
Алайда 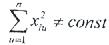 кезінде ортогоналды орталық-композициялық жоспарлар (ООКЖ) факторлық кеңістіктің түрлі нүктелеріндегі отклик дисперсиясының тұрақтылығын қамтамасыз етпейді.
кезінде ортогоналды орталық-композициялық жоспарлар (ООКЖ) факторлық кеңістіктің түрлі нүктелеріндегі отклик дисперсиясының тұрақтылығын қамтамасыз етпейді.
Сәйкесінше, бірдей дисперсиялы отклик мәнін жоспар орталығынан тең қашықтықта анықтауға мүмкіндік беретін жоспар қажет, ондай жоспар рототабелді деп аталады.
Толық факторлы эксперимент (ТФЭ) жоспарларының қарастырылып отырған нұсқалары сынақтың өте көп санымен негізделеді. Факторлық экспериментті жоспарлау теориясы зерттеу шынайылығына зиян келтірмей, сынақ санын азайту мүмкіндігіне ие.
Мұндай әдіске эксперименттің бөлшекті факторлық жоспары жатады (БФЭ). БФЭ 2k ТФЭ бөлігі немесе реплика үлесі болып табылады. ТФЭ тең жартысы болатын (1/2nk=2k-1) эксперимент ТФЭ жарты репликасы; ТФЭ ¼-не тең (1/4nk=2k-2) БФЭ кезіндегі эксперимент 2k ТФЭ-тің ширек репликасы деп аталады т.б. Бұл кезде бөлшекті репликалар ортогоналдылық, нормалдық және баланс қасиеттеріне ие болуы керек, бұл шарт сақталад, себебі БФЭ құру үшін алдымен аз санды факторларды сынау мақсатында ТФЭ құрылады, содан кейін факторлардың статистикалық маңызсыз өзара әрекеті әсері қалған факторларға ауыстырылады. Мәселен, 24 ТФЭ-тен жарты реплика түрінде, яғни төрт факторлы үдерісті зерттеу жоспарын құру кезінде  регрессиясы теңдеуінде
регрессиясы теңдеуінде 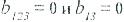 коэффициенттері статистикалық тұрғыда маңызды емес деп есептейміз. 24 ТФЭ матрицасын құрып (4.10 кесте) барлық мәні х4=+1 болатын сегіз төменгі жолды ерекшелейміз.
коэффициенттері статистикалық тұрғыда маңызды емес деп есептейміз. 24 ТФЭ матрицасын құрып (4.10 кесте) барлық мәні х4=+1 болатын сегіз төменгі жолды ерекшелейміз.
Кесте 4.10 24 ТФЭ матрицасы
| Сынақ № | Факторлар деңгейі | Сынақ № | Факторлар деңгейі | ||||||
| х1 | х2 | х3 | х4 | х1 | х2 | х3 | х4 | ||
| - | - | - | - | - | - | - | + | ||
| + | - | - | - | + | - | - | + | ||
| - | + | - | - | - | + | - | + | ||
| + | + | - | - | + | + | - | + | ||
| - | - | + | - | - | - | + | + | ||
| + | - | + | - | + | - | + | + | ||
| - | + | + | - | - | + | + | + | ||
| + | + | + | - | + | + | + | + |
24-1 БФЭ матрица-жоспары (4.11 кесте) 24 ТФЭ матрицасы негізінде құрылады, онда х4 орнына х1, х2, х3 өзара үштік әрекет әсері жазылады және қос өзара әсер бағаны толтырылады. 9,10 және 11 бағандар үш өзара әрекет әсерімен толтырылады, ал 12 баған факторлардың төртінші өзара әрекет әсерімен толтырылады. Кестені талдай келе, 4 және 9; 2 және 10; 3 және 11 бағандар ұқсас екенін аңғарамыз (4.11) кестеде бағыттауышпен көрсетіледі). Бұл жерде 12 баған х0 жалған ауыспалы бағанға ұқсас (4.11 кестеде х0 бағаны көрсетілмеді).
БФЭ жоспарлау әдісінің артықшылығы анық байқалады – зерттеу нақтылығына зиян келтірілмей сынақ саны айтарлықтай қысқарады, әсіресе, бұл артықшылық көп санды факторлармен болатын үдерісті зерттеу кезінде байқалады (бұл жерде өзара әрекет әсері әлсіз байқалатыны белгілі болуы керек).
Кесте 4.11 - 24-1 бөлшекті факторлы эксперимент матрицасы
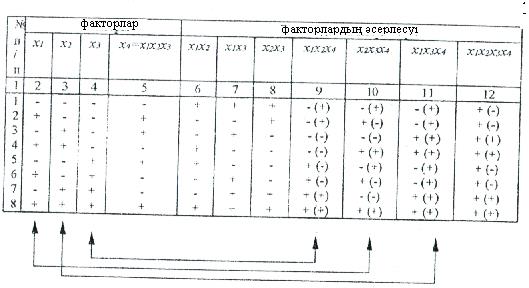
Алайда кемшіліктер де кездеседі, олардың негізгілері жоспар бағандарының ұқсастығы, регрессия коэффициенті бағаларын араластыру әсерін тудырады, оны төмендегі қатынасты білдіретін жетекші қатынасты (ЖҚ) енгізу арқылы анықтауға болады:
х4=х1х2х3
 Бұл β123 коэффициенті орнына b4 бағаланатынын, яғни факторлардың сызықтық әсері мен х1х2х3 үш өзара әрекетінің орнын ауыстыратынын білдіреді. Шартты түрде b4 β4 + β123 деп жазылады, яғни коэффициент бағасына β123 үш өзара әрекет бағасы қосылады.
Бұл β123 коэффициенті орнына b4 бағаланатынын, яғни факторлардың сызықтық әсері мен х1х2х3 үш өзара әрекетінің орнын ауыстыратынын білдіреді. Шартты түрде b4 β4 + β123 деп жазылады, яғни коэффициент бағасына β123 үш өзара әрекет бағасы қосылады.
Басқа бағалардың ауысу әсерін анықтау үшін анықтағыш контраст (АК) түсінігі енгізіледі, ол жаңа х4 факторына көбейтілген жетекші қатынасты білдіреді. Мәселен 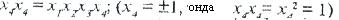
Сызықты әсер мен қос өзара әрекет бағасын ауыстырып, мәселен, 24-1 БФЭ (4.11 кесте) екі бөлігін де кезектеп х1, х2, х3 мәніне көбейту арқылы х1х2, х1х3 және х2х3 мәнін аламыз.
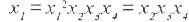 ... (2 және 10 бағандар ұқсас)
... (2 және 10 бағандар ұқсас)
 (3 және 11 бағандар ұқсас)
(3 және 11 бағандар ұқсас)
 (4 және 9 бағандар ұқсас)
(4 және 9 бағандар ұқсас)
....
.....
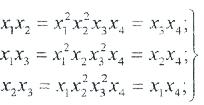 Кестеде көрсетілмеген
Кестеде көрсетілмеген
Сәйкесінше,
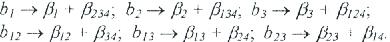
Формула
Бөлшекті реплика әдісін пайдаланып, фактор санын азайтуға болады. b1 регрессия коэффициенті санына тең экспериментте сынақ санымен жоспар толық деп аталады. Бұл әдіс (жоспар) негізінен көп санды факторлармен болатын үдерістер (нысандар) сызықты моделін құру үшін қолданылады. Сондай-ақ отклик беті көп факторлы үдерісті алғашқы жанасуда зерттеу кезінде шекті линеаризациялы көпфакторлы кеңістік саласында гипер жазықтықтан аз ғана ерекшеленетін кезде қолданылады.
Оптимумды іздеу. Көп зерттеулерде зерттелетін нысан, үдеріс, құбылыс және т.б. оңтайландыруды, яғни фнукция максимум және минимум мәніне ие болатын жағдайдағы фактор мәнін табуды мақсат ететід. Жоспарлау теориясы оңтайландыру міндетін шешу мүмкіндігіне негізделеді және ол әдетте екі кезеңде шешіледі.
Бірінші кезең Wі факторлы кеңістіктің өнімді саласынан максимум немесе минимум стационарлық нүктесі саласына шығудан тұрады. Бұл жағдайда толық факторлы эксперимент және факторлардың өзара әрекет әсері есебімен бөлшекті факторлы эксперимент қолданылады.
Зерттеу үдерісін оңтайландырудың екінші кезеңі, оптиуму нүктесіне қозғалыс тіке шығу әдісімен жүзеге асырылады. Бұл әдісті агрегатты оңтайландыру үлгісінде қарастырамыз. Зерттеу пәні болып агрегат қармауышының ені (фактор х1) және оның қозғалыс жылдамдығы (фактор х2) оңтайлы мәнге тең және бұл жағдайда оның өнімділігі (у оңтайландыру параметрі) максималды болатын (немесе агрегат жұмысы бірлігіне шығын минималды болатын) мәнді іздеу табылады. Сөйтіп, екіфакторлы эксперимент мысалында тіке шығу әдісімен (Бокс-Уилсон әдісі) у=уmax нүктесіне градиентті бағыттауда отклик беті бойынша қозғалыс қарастырылды. У = f(x1x2…) қандай да бір функциясының градиенті деп у шамасының өзгерісінің ең үлкен жылдамдығын білдіретін вектор аталады. Градиент бағыты у (х1х2...) =const деңгейі бетінің осы нүкте арқылы өтетін нормалы бағытына сай келеді, grad y деп белгіленеді және мынаған тең болады:
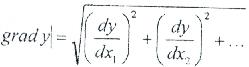
Қозғалыс сәйкесінше, «қадамдап» жасалады.
суретте шығысы у =const-қа тең қисық сызықты отклик беті көрсетілген. у=max оңтайландыру параметрінің оңтайлы мәнін іздеу бағыты. 0і басқы нүктеден 1, 2, 3, 4 нүктелерінде сынақ тәжірибе бойынша есептелетін V і градиенті желісімен жүзеге асырылады. Нәтижесінде регрессия теңдеуін, мәселен.... түріндегі теңдеуді алады. Егер Vі векторы арқылы өтетін жазықтық откликі бетін тарататын болсақ, 02 нүктесінде У максимумды қисық сызық аламыз (4.7 б сурет). Vі векторы бойынша қозғалыс 02 максимум нүктесіне дейін жетеді. Тіке шығу кезінде Vі градиенті бойымен қозғалыстың һ қадамының сандық мәні маңызды (4.7 б сурет) өлшемі бойынша кіші қадамдар сынақтың көп санын береді, үлкен қадамда үлкен мән нүктесін (02 нүктесін) аттап өтуге болады. Бұл жерде әр қадамда нақты тәжірибе жүргізудің қажет еместігін ескеру керек. Сынақ санын азайту үшін у параметрі шамасын есептемей бірнеше қадам жасауға болады. Бұл қадамдар ойша жасалған сынақтар деп аталады. Бірнеше ойша жасалған сынақтан соң нақты тәжірибе орындалады.

Сурет 4.7 Тіке шығу әдісі сызбасы
Х ауыспалысы (факторы) бағытына әр қадам b1 коэффициентіне пропорционал және һх1=kb-ге тең болуы керек.
Мұндағы k – алдында баяндалған шарттан таңдалған пропорционалдылық коэффициенті одан әрі 02 нүктесі айналасында (4.7 а сурет) 1; 2; 3; 4 нүктелерінде сынақтар сериясын жүргізеді, нәтижесінде жаңа теңдеу, b1 коэффициентінің жаңа мәні және отклик беті осы қимасында у максимумының 03 нүктесіне 2 векторы бойынша оптиумуға шығудың жаңа бағыты анықталады. Мұндай теңдеулерде b1 коэффициенттері х1 бағытында бет көлбеуін сипаттайды және факторлардың сызықтық әсері деп аталады. Һ1 қадамы вектор бойымен оның қимасының қисық сызығы бойынша қозғалу кезінде максимумды (02, 03 және т.б. нүктелерді) «аттапөтпейтіндей» етіп таңдалады. 03 нүктесі жанында (1’’, 2’’, 3’’, 4’’ нүктелерінде) сынақтардың 3-ші сериясын жүргізеді. b1 коэффициентінің мәні мен отклик бетінің максимум саласына шығатын V3 градиенті бағыты тағы анықталады.
Осымен тіке шығу үдерісі аяқталып, максимум саласында отклик бетін барынша мұқият тексеру басталады – сипаттамасы беттің қисық сызығын сипаттайтын екінші, кейде үшінші тәртіптегі теңдеудің (математикалық үлгінің) стационарлық саласындай.
Іріктеу (таңдау) көлемін жоспарлау.
Экспериментте іріктеу көлемі бірнеше факторға, оның ішінде өзгерістің қандай дәрежесін – сандық не сапалық дәрежесін бағалау керектігіне байланысты. Бұл екі жағдайда іріктеу көлемін анықтау әдістемесі әртүрлі. Іріктеу көлемін анықтаудың негізгі міндеті болып минималды, бірақ зерттеу нысаны туралы барынша толық ақпарат алуға мүмкіндік беруге қажетті сынақ санын анықтау табылады. Өлшеу саны (іріктеу көлемі) тым аз болғанда сынақтың нақты көлемі де ұлғаяды. Осыған орай, іріктеу көлемін оңтайландыру, яғни сенімді ықтималдылықтың белгілі бір деңгейінде статикалық шынайы нәтиже алу мүмкіндігін беретін бақылау санын анықтау керек.
Іріктеу көлемін анықтайтын бірнеше формула бар, олардың ішінде ең қарапайым және шынайысын ұсынуға болады.
 (4.21)
(4.21)
Мұндағы:
t – [23], [25] және т.б. кестелер бойынша Стьюдент критерийінің стандартты мәні;
V – түрлендіру коэффициенті, %.
 - шекті қатысты қателік, %.
- шекті қатысты қателік, %.
Егер Сьюдент критерийі бойынша деректер болмаса, оның шамалас мәнін төмендегі формула бойынша 0,95 ықтималдық деңгейі кезінде және n’ шамалас сынақ санына байланысты егістік сынақтары үшін қажетті нақтылықта табуға болады:
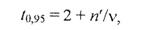
Мұндағы v=n’-1 –еркіндік дәрежесі саны.
Мысалы, n=5t0.95 = 2+5/4 кестедегі t=3,24 мәніне сәйкес келеді. Іс жүзінде t көп өзгермейтін және ықтималдық деңгейі 0,95t=2, 099t=2.6 тең n’>30 таңдалады.


 Шекті қатысты қателік мәні сынақтың жоспарлану нақтылығына байланысты болады. Сынақ нақтылығы жоғары болғанда, мысалы, құрал жасауда = 3…5%, орташа нақтылықта (машина жасауда) = 5…6%, ауылшаруашылық машиналарын егістік жағдайында сынау кезінде
Шекті қатысты қателік мәні сынақтың жоспарлану нақтылығына байланысты болады. Сынақ нақтылығы жоғары болғанда, мысалы, құрал жасауда = 3…5%, орташа нақтылықта (машина жасауда) = 5…6%, ауылшаруашылық машиналарын егістік жағдайында сынау кезінде 
 = 10 % талабын қанағаттандырады.
= 10 % талабын қанағаттандырады.
Түрлендіру коэффициенті:
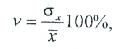
Мұндағы: σ – сынақ мәнінің орташа квадратты ауытқуы;
Х – осы мәндер қатарының орташа арифметикалық мәні (σ және х есебін 4.5 бөлімнен қараңыз).
 Сөйтіп, (4.21) мәніне сай, мысалы, t=2,6; v=24 % және = 10% кезінде:
Сөйтіп, (4.21) мәніне сай, мысалы, t=2,6; v=24 % және = 10% кезінде:
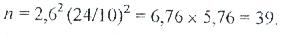
Дата добавления: 2015-05-05; просмотров: 6265;
