Необмежена двопровідна система
Розглянемо фізичну сутність процесів, що відбуваються в системі Лехера відповідно з [6]. Візьмемо до уваги, що поперечні розміри системи є досить малими порівняно з довжиною хвилі. Це означає, що вздовж поперечного напрямку електромагнітне поле можна вважати квазістаціонарним. У той самий час вважаємо, що проводи є довгими – на їх довжині повинно укладатися щонайменше кілька хвиль. Тому електричні струми в проводах не квазістаціонарні, сила струму 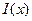 ,а також лінійна густина електричного заряду
,а також лінійна густина електричного заряду 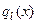 істотно змінюються вздовж них (вісь X спрямована паралельно проводам). Унаслідок симетрії струм
істотно змінюються вздовж них (вісь X спрямована паралельно проводам). Унаслідок симетрії струм 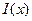 , що проходить вздовж одного з проводів, є рівним і протилежно спрямованим струму, що проходить навпроти нього вздовж іншого проводу (рис. 5.3.1, стрілками позначено напрямок електричних струмів у деякий момент часу). Аналогічно розміщуються й електричні заряди на проводах. Електричну напругу між проводами, виміряну вздовж перпендикуляра до них, будемо позначати через
, що проходить вздовж одного з проводів, є рівним і протилежно спрямованим струму, що проходить навпроти нього вздовж іншого проводу (рис. 5.3.1, стрілками позначено напрямок електричних струмів у деякий момент часу). Аналогічно розміщуються й електричні заряди на проводах. Електричну напругу між проводами, виміряну вздовж перпендикуляра до них, будемо позначати через 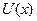 .
.
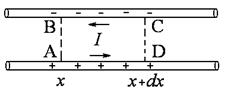
Рисунок 5.3.2 – До розрахунку напруги та струму в двопровідній системі
Розглянемо на одному з проводів системи Лехера нескінченно малий відрізок 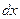 (рис. 5.3.2). Через точку А за час
(рис. 5.3.2). Через точку А за час 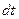 усередину розглянутого відрізку входить електричний заряд
усередину розглянутого відрізку входить електричний заряд 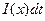 , а через точку D виходить заряд
, а через точку D виходить заряд 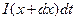 . Різниця заряду, що входить, над зарядом, що виходить, становить
. Різниця заряду, що входить, над зарядом, що виходить, становить 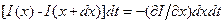 . Виходячи із закону збереження електричного заряду, ця величина дорівнює зміні заряду всередині розглянутого відрізку
. Виходячи із закону збереження електричного заряду, ця величина дорівнює зміні заряду всередині розглянутого відрізку 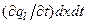 (нагадаємо, що тут
(нагадаємо, що тут 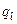 – густина електричного заряду). Таким чином,
– густина електричного заряду). Таким чином,
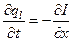 . (5.3.1)
. (5.3.1)
Застосуємо тепер до контуру ADCBрівняння Максвелла:
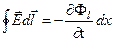 , (5.3.2)
, (5.3.2)
де 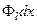 – магнітний потік[22]), що пронизує цей контур. Інтеграли на окремих відрізках контуру ADCB дорівнюють
– магнітний потік[22]), що пронизує цей контур. Інтеграли на окремих відрізках контуру ADCB дорівнюють
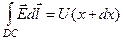 ,
, 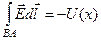 ,
,
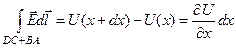 ,
,
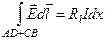 , (5.3.3)
, (5.3.3)
де 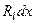 – сумарний опір елементів проводів AD і СВ. У співвідношеннях (5.3.3)
– сумарний опір елементів проводів AD і СВ. У співвідношеннях (5.3.3) 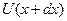 – напруга між точками D та C,
– напруга між точками D та C, 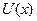 – напруга між точками B та A. Тоді з (5.3.2) та (5.3.3) отримуємо
– напруга між точками B та A. Тоді з (5.3.2) та (5.3.3) отримуємо
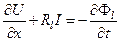 . (5.3.4)
. (5.3.4)
Нагадаємо, що величини 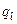 ,
, 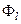 і
і 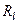 – це заряд, магнітний потік і опір одиниці довжини двопровідної лінії. Далі припускаємо, що опір
– це заряд, магнітний потік і опір одиниці довжини двопровідної лінії. Далі припускаємо, що опір 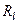 дорівнює нулю. Використаємо тепер умову квазістаціонарності для поперечних характеристик системи. Позначимо через
дорівнює нулю. Використаємо тепер умову квазістаціонарності для поперечних характеристик системи. Позначимо через 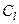 ,
, 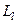 відповідно ємність та індуктивність одиниці довжини лінії. Цівеличини знайдемо зі співвідношень
відповідно ємність та індуктивність одиниці довжини лінії. Цівеличини знайдемо зі співвідношень
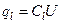 ,
, 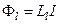 . (5.3.5)
. (5.3.5)
Вилучивши з рівнянь (5.3.1), (5.3.4) 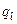 і
і 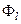 та враховуючи, що
та враховуючи, що 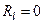 , отримаємо
, отримаємо
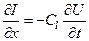 , (5.3.6)
, (5.3.6)
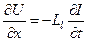 . (5.3.7)
. (5.3.7)
Вилучивши із системи рівнянь (5.3.6), (5.3.7) або силу струму, або напругу, отримаємо відповідні хвильові рівняння
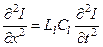
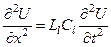 . (5.3.8)
. (5.3.8)
Це означає, що вздовж двопровідної системи Лехера поширюється хвиля струму та напруги з фазовою швидкістю
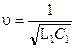 . (5.3.9)
. (5.3.9)
Для тонких циліндричних проводів радіусом 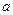 , відстань між якими дорівнює
, відстань між якими дорівнює  , індуктивність та ємність дорівнюють
, індуктивність та ємність дорівнюють
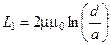 ,
, 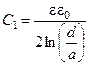 . (5.3.10)
. (5.3.10)
Підставляючи (5.3.10) до (5.3.9), отримуємо
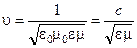 , (5.3.11)
, (5.3.11)
де 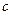 – швидкість світла у вакуумі. Таким чином, фазова швидкість поширення хвиль струму, напруги у двопровідній лінії
– швидкість світла у вакуумі. Таким чином, фазова швидкість поширення хвиль струму, напруги у двопровідній лінії 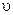 збігається зі швидкістю поширення електромагнітних хвиль у вільному просторі.
збігається зі швидкістю поширення електромагнітних хвиль у вільному просторі.
Вище ми не вводили ніяких припущень про форму коливань і хвиль у системі Лехера. Будемо вважати далі, що коливання і хвилі гармонічні. У випадку біжучої хвилі струм 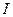 та напруга
та напруга 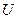 коливаються в однакових фазах. Це безпосередньо випливає зі співвідношень (5.3.6), (5.3.7). Змінні струм, напруга створюють змінні електричне та магнітне поля. Неважко з’ясувати, що в біжучій хвилі вектори напруженості електричного та магнітного полів перпендикулярні до проводів, їх початкові фази коливань збігаються з відповідними фазами струму
коливаються в однакових фазах. Це безпосередньо випливає зі співвідношень (5.3.6), (5.3.7). Змінні струм, напруга створюють змінні електричне та магнітне поля. Неважко з’ясувати, що в біжучій хвилі вектори напруженості електричного та магнітного полів перпендикулярні до проводів, їх початкові фази коливань збігаються з відповідними фазами струму 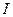 та напруги
та напруги 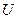 .
.
Дата добавления: 2015-05-05; просмотров: 669;
