Теплоемкость. Удельная теплоемкость – теплота, которую надо сообщить 1 кг вещества для повышения его температуры на 1 К:

Удельная теплоемкость – теплота, которую надо сообщить 1 кг вещества для повышения его температуры на 1 К:

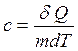, (11.10)

где т – масса вещества.

Пользуются также понятием молярной теплоемкости (для одного моля вещества):

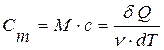, (11.11)

где М – молярная масса вещества, v – количество молей вещества.

Если известны удельная и молярная теплоемкость вещества, то теплоемкость конкретного тела можно определить как 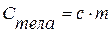или .

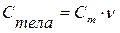Различают теплоемкости при постоянном давлении и при постоянном объеме. Для ИГ, рассматривая уравнение (11.4) совместно с уравнением (11.3) и (11.5), получают, что при постоянном объеме молярная теплоемкость равна

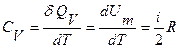, (11.12)

а при постоянном давлении -

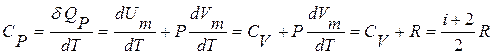. (11.13)

Уравнение (11.13)- уравнение Ю.Р.Майера (1814–1878): выводится с учетом уравнения Менделеева–Клапейрона РV_m=RT и РdV_m+V_mdР= РdV_m=RdT при постоянном давлении.

При сравнении уравнений (11.12) и (11.13) видно, что молярная теплоемкость при постоянном давлении больше, т.к. часть подводимой теплоты расходуется еще и на совершение ИГ работы расширения (против внешних сил).

На практике часто используют отношение теплоемкостей 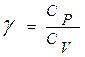(показатель адиабаты или показатель Пуассона). Так как 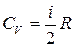и 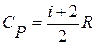_, то для одноатомного газа i=3 и показатель адиабаты ; для двухатомного i=5 и показатель Пуассона 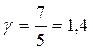; для трех- и более – i=6 и .

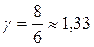Приведенные выше рассуждения классической (не квантовой) теории теплоемкости справедливы лишь для ИГ, т.е. в ряде частных случаев, и потому ограниченно применимы.