Применение первого начала термодинамики к изопроцессам. Адиабатический и политропный процессы
Изопроцессомназывается процесс, при протекании которого остаются постоянными масса газа m и любой из его параметров состояния (P, V или T). При 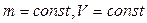 процесс называется изохорным. Согласно формуле (11.5), работа при изохорном процессе равна
процесс называется изохорным. Согласно формуле (11.5), работа при изохорном процессе равна
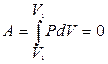 . (11.15)
. (11.15)
Формула (11.4) с учетом формул (11.3) и (11.15) имеет вид
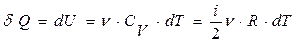 . (
. ( 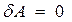 ) (11.16)
) (11.16)
При 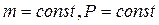 процесс называется изобарическим. Согласно формуле (11.5) работа при изобарном процессе равна
процесс называется изобарическим. Согласно формуле (11.5) работа при изобарном процессе равна
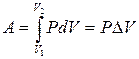 . (11.17)
. (11.17)
Формула (11.4) с учетом формул (11.3) и (11.17) имеет вид
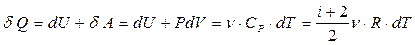 . (11.18)
. (11.18)
При 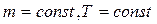 процесс называется изотермическим (dT=0). Согласно формуле (11.5) работа при изотермическом процессе равна
процесс называется изотермическим (dT=0). Согласно формуле (11.5) работа при изотермическом процессе равна
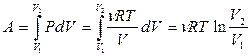 . (11.19)
. (11.19)
Формула (11.4) с учетом формул (11.3) и (11.19) имеет вид
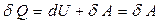 . (11.20)
. (11.20)
Следует заметить, что при недостатке подвода теплоты из внешней среды работа расширения ИГ может совершаться и за счет убыли внутренней энергии ИГ, и, следовательно, его температура понизится.
Адиабатным называется процесс, протекающий без теплообмена с окружающей средой ( 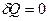 ). Адиабатными можно считать процессы, происходящие в камере сгорания тепловых двигателей, распространение звуковых волн в газах и т.д.
). Адиабатными можно считать процессы, происходящие в камере сгорания тепловых двигателей, распространение звуковых волн в газах и т.д.
Быстрое адиабатное сжатие воздуха в двигателях типа «дизель» приводит к повышению температуры дизеля до 500–600°С и к самовоспламенению при впрыске топлива. Первое начало термодинамики в случае адиабатного процесса имеет вид: 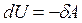 , которое с учетом формул (11.3) и (11.5) можно записать так:
, которое с учетом формул (11.3) и (11.5) можно записать так:
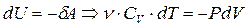 . (11.21)
. (11.21)
Уравнение адиабатного процесса:
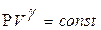 , (11.24)
, (11.24)
где 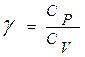 (показатель адиабаты или показатель Пуассона).
(показатель адиабаты или показатель Пуассона).
С использованием уравнения Менделеева–Клапейрона можно получить связь параметров V и T, Р и T при адиабатном процессе:
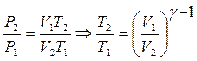 или
или 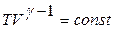 , (11.25)
, (11.25)
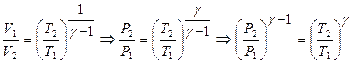 или
или 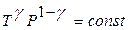 . (11.26)
. (11.26)
Работа при адиабатическом процессе:
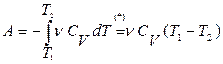 . (11.27)
. (11.27)

Рис. 11.2
Переход (*) соответствует идеальному случаю, в общем случае теплоемкость равенства 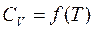 и интегрирование усложняется. Работа при адиабатическом процессе меньше, чем при аналогичном изотермическом (см. площади под кривыми, рис. 11.2).
и интегрирование усложняется. Работа при адиабатическом процессе меньше, чем при аналогичном изотермическом (см. площади под кривыми, рис. 11.2).
С учетом равенства 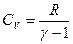 из формулы (11.13) и
из формулы (11.13) и 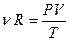 из уравнения Менделеева–Клапейрона выражение (11.27) примет вид
из уравнения Менделеева–Клапейрона выражение (11.27) примет вид
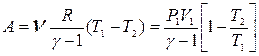 . (11.28)
. (11.28)
Рассмотренные выше процессы – изохорный, изобарный, изотермический, адиабатный – можно записать одним уравнением – уравнением политропного процесса:
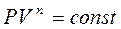 , (11.29)
, (11.29)
где n – показатель политропы (все эти процессы называются политропными), т.е.:
а) V=const, C=CV , n=-¥ 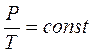 ;
;
б) P=const, C=CP, n=0 PV0=const;
в) T=const, C= 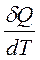 =¥, n=1 PV=const;
=¥, n=1 PV=const;
г) 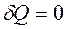 ; C=0, n =
; C=0, n = 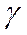
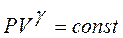 .
.
Дата добавления: 2015-05-05; просмотров: 1007;
