Газ Ван-дер-Ваальса.

Наиболее известным уравнением состояния реальных газов, учитывающим собственный объем молекул газа и их взаимодействие, является уравнение (1873г.) нидерландского физика И.Д. Ван-дер-Ваальса (1837–1923). Рассмотрим коротко вывод этого уравнение.

Конечный объем (размеры) молекул увеличивает давление реального газа по сравнению с ИГ, т.к. передача импульса стенкам через пространство сосуда осуществляется быстрее, чем точечными молекулами вследствие прохождения ими между столкновениями меньшего пути. Учитывают только (силы отталкивания) парные столкновения молекул – столкновение двух молекул, когда остальные на них не действуют. Вероятностью и влиянием одновременных тройных, четверных и т.д. столкновений пренебрегают. При расчете давления можно считать, что одна молекула остается неподвижной, а другая движется с удвоенной кинетической энергией. При столкновении центры молекул могут сблизиться на расстояние, меньшее d – диаметр молекулы, поэтому можно считать неподвижную молекулу окруженной сферой ограждения радиуса d, а движущуюся молекулу точечной. Если применить такое приближение к газу из N молекул, то половина молекул N/2 будет покоится (окружена сферами ограждения), а другая половина может рассматриваться как газ из N₁=N/2с температурой T₁=2T. Этому газу был бы доступен объем сосуда V за исключением объема b всех сфер ограждения N/2 покоящихся молекул, т.е. V–b. Тогда согласно уравнению (9.12), давление, оказываемое этими молекулами на стенку сосуда, имеет вид

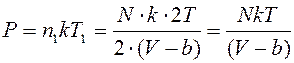
или для одного моля газа .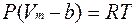

Рис. 13.2

Очевидно, что объем b приблизительно равен учетверенному объему всех молекул газа (рис. 13.2). Учтем теперь действие сил притяжения между молекулами газа. Когда молекула находится внутри вещества (газа), то силы притяжения со стороны остальных молекул со всех сторон примерно скомпенсированы. Если же молекула находится в поверхностном слое, то появляется некомпенсированная сила притяжения F, направленная от поверхности внутрь газа. Под действием этих сил молекула может вообще не долететь до стенки сосуда, а отразиться от поверхностного слоя вещества. Действие сил притяжения создает добавочное – внутреннее или молекулярное давление P_i~N_сл F, где N_сл – число молекул в приповерхностном (пристеночном) слое. Величины N_сл и F прямо пропорциональны плотности и обратно пропорциональны объему газа. Для одного моля газа P_i=а/V_m² и реальное давление газа равно 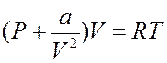, где Р – давление ИГ. Для неплотных газов поправки на силы отталкивания и притяжения можно вводить независимо, тогда обобщая, получим

(13.2)

или для произвольного количества вещества с учетом V=nV_m:

. (13.3)

Уравнение (13.3)– уравнение Ван-дер-Ваальса, a и b – константы, поправки Ван-дер-Ваальса.

Уравнение (13.2), рассматриваемое как уравнение для определения объема при данных Т и Р, есть уравнение третьей степени, в преобразованном виде оно имеет вид

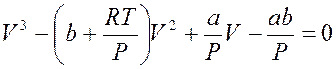. (13.4)

Так как уравнение третьей степени с вещественными коэффициентами может иметь либо один вещественный корень и два комплексно сопряженных, либо три вещественных корня, то на плоскости PV прямая, параллельная оси V, может пересекать изотерму либо в трех точках, либо в одной. Построение по точкам изотермы Ван-дер-Ваальса приводит к семейству кривых, изображенных на рис. 13.3 (теоретически Ван-дер-Ваальс, экспериментально Т. Эндрюс (1813–1885) для СО₂).

Левая, круто спадающая ветвь соответствует малому изменению объема при изменении давления, что характерно для жидкого состояния вещества. Правая пологая ветвь соответствует значительному изменению объема при изменении давления, что соответствует газообразному состоянию вещества.

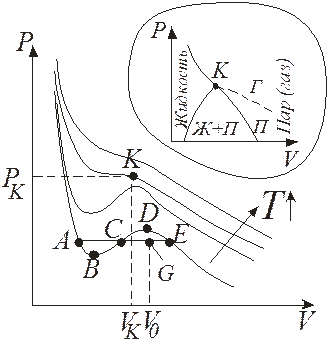
Рис. 13.3

Переход из жидкого в газообразное состояние и обратно происходит не вдоль изотермы Ван-дер-Ваальса, а вдоль изобары АЕ, которая одновременно является и изотермой реального газа. При этом площади фигур АВС и СDЕ равны (правило Максвелла). Точки изотермы А и Е изображают двухфазные состояния вещества, а между ними существуют одновременно две фазы. Чем ближе изображающая точка G к А, тем больше в системе жидкости, чем ближе к Е – тем больше пара. Если обозначить максимальный объем моля жидкости и минимальный объем пара в системе при температуре Т через V₁ и V₂ соответственно, а объем двухфазной области в точке G через V₀, то 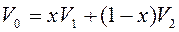, где х – мольная доля жидкости в состоянии G; отсюда, зная объем V₀, можно найти и долю x жидкости. Участки АВ и DЕ изотермы Ван-дер-Ваальса изображают метастабильные состояния вещества: переохлажденную жидкость и пересыщенный пар, которые могут существовать при известных условиях (при очень медленном квазиравновесном проведении процесса и тщательной подготовки, например, удалении всех загрязнений из объема нагреваемой жидкости и со стенок сосуда, т.к. процесс кипения начинается легче на посторонних частицах – включениях). Участок ВD соответствует абсолютно неустойчивым (рост давления при росте объема) состояниям вещества и ни при каких условиях не реализуется. При достаточно низких температурах участок АВС может опускаться ниже оси OV, что адекватно отрицательному давлению, соответствующему состоянию растянутой жидкости (за счет действия сил поверхностного натяжения).

С ростом температур область горбов и впадин на изотерме Ван-дер-Ваальса уменьшается и при температуре Т_к – критической температуре – превращается в точку перегиба с горизонтальной касательной. Для этой точки уравнение (13.4) имеет три одинаковых корня и принимает вид 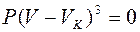. Критические параметры данного газа определяют по формулам

, , ,

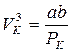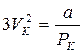откуда

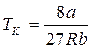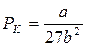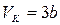, , . (13.5)

Если провести через крайние точки горизонтальных участков семейства изотерм реальных газов кривые, то получим диаграмму PV (см. вставку на рис.13.3), по которой можно легко наглядно определить, в каком из состояний при данной температуре будет находиться вещество. Следует отметить, что отличие пара от других газообразных состояний заключается в том, что при изотермическом сжатии пар претерпевает процесс сжижения. Газ же, при температуре выше критической, не может быть превращен в жидкость ни при каком давлении.