Энтропия. Второе начало термодинамики.
Необратимость тепловых явлений, на первый взгляд, кажется парадоксальным. Действительно, ведь все тепловые процессы сводятся к механическим (движению и взаимодействию молекул), а механические явления – обратимы. В чем причина необратимости тепловых процессов? Ответ на этот вопрос дает статистическая теория, основанная на теории вероятности.
| Необратимость процессов можно показать на простом примере перемешивания 10 черных и 10 белых шаров. При встряхивании шары перемешиваются. После встряхивания (рис. 12.2,а) практически никогда не удается получить исходного упорядоченного (рис. 12.2,б) распределения шаров. |  Рис. 12.2
Рис. 12.2
|
Каким образом шары «знают», что им необходимо распределяться в беспорядке? Пусть после встряхивания в верхнем ряду оказалось три белых шара (в нижнем – три черных). Какими способами может быть реализовано данное распределение?
Перебором выясняют возможные комбинации расположения белых шаров в верхнем ряду:
| Белые шары в нижнем ряду, шт. | Белые шары в верхнем ряду, шт. | Число комбинаций, с помощью которых может быть получено данное состояние |
Максимальное число комбинаций соответствует равномерному, наиболее неупорядоченному распределению шаров (5 – 5) и, следовательно, наиболее вероятному. Из примера видно, что причина необратимости кроется в малой вероятности упорядоченных состояний. Термодинамической вероятностью W данного состояния системы называется число комбинаций – (микро)состояний отдельных элементов системы, реализующих данное (макро)состояние системы. Таким образом, ТД вероятность служит величиной, характеризующей направленность протекания процессов.
Первоначально считали, что самопроизвольно могут протекать только процессы с выделением теплоты (например, только экзотермические реакции), однако после открытия самопроизвольно протекающих эндотермических реакций оказалось, что это не так: тепловой эффект не может служить достаточным критерием определения направления протекания процесса. Поэтому был проведен поиск достаточного критерия, который однозначно давал бы ответ о направлении протекания процессов.
Сравнивая ТД вероятность различных состояний, установили, что процессы протекают в направлении от менее вероятных состояний к более вероятным. Вычисление ТД вероятностей на практике – очень сложная задача, поэтому в середине прошлого века немецкий физик Л.Больцман ввел необходимую физическую величину, которую назвали энтропией.
Энтропия S, как и ТД вероятность W, характеризует направленность процессов и является мерой беспорядка системы: чем больше энтропия, тем ближе система к наиболее вероятному – равновесному состоянию (ему соответствует максимальная неупорядоченность). Больцман показал, что энтропия пропорциональна ТД вероятности:
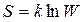 , (12.4)
, (12.4)
где k – коэффициент пропорциональности, 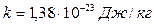 – постоянная Больцмана.
– постоянная Больцмана.
Энтропия, как функция, полностью определяется состоянием (параметрами) системы, не зависит от способа перехода из состояния в состояние, т.е. является функцией состояния и полным дифференциалом. Она может быть определена как
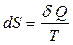 (12.5)
(12.5)
или, применяя первое начало термодинамики для идеальных газов,
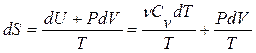 (12.6)
(12.6)
или 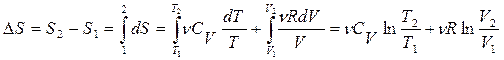 . (12.7)
. (12.7)
Наименьшей энтропией обладает идеальный кристалл при 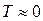 К, т.к. при этом атомы практически неподвижны в узлах кристаллической решетки. При повышении температуры (при нагревании
К, т.к. при этом атомы практически неподвижны в узлах кристаллической решетки. При повышении температуры (при нагревании 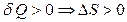 ) атомы в узлах решетки колеблются все интенсивнее, а при плавлении или, тем более, возгонке (испарении из твердого состояния в газообразное), парообразовании над расплавом могут занимать различные положения (возрастание энтропии), при охлаждении же, наоборот,
) атомы в узлах решетки колеблются все интенсивнее, а при плавлении или, тем более, возгонке (испарении из твердого состояния в газообразное), парообразовании над расплавом могут занимать различные положения (возрастание энтропии), при охлаждении же, наоборот, 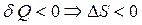 . Например, при плавлении вещества изменение энтропии определяется как сумма изменений энтропии при нагревании до температуры плавления и при плавлении вещества:
. Например, при плавлении вещества изменение энтропии определяется как сумма изменений энтропии при нагревании до температуры плавления и при плавлении вещества:
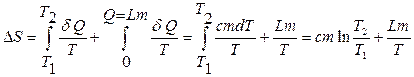 ,
,
где L – удельная теплота плавления вещества.
Для адиабатного процесса 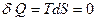 , т.е. адиабатный процесс является изоэнтропийным.
, т.е. адиабатный процесс является изоэнтропийным.
В обратимом процессе при переходе из состояния 1 в 2 энтропия не зависит от способа перехода. Для циклов T1=T2, V1=V2, Р1=Р2, следовательно, 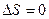 . В статистической физике доказывают, что для любого обратимого процесса, происходящего в замкнутой системе
. В статистической физике доказывают, что для любого обратимого процесса, происходящего в замкнутой системе 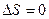 , а для необратимого –
, а для необратимого – 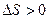 , т.е. в замкнутой системе энтропия не убывает. Обобщенно это можно записать неравенством Клаузиуса
, т.е. в замкнутой системе энтропия не убывает. Обобщенно это можно записать неравенством Клаузиуса
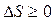 , (12.8)
, (12.8)
которое является математической формой записи второго начала термодинамики:в любом процессе система стремится к наиболее вероятному состоянию. Можно по-иному сформулировать II закон термодинамики: невозможен такой круговой процесс, единственным результатом которого были бы:
– превращение теплоты, полученной от нагревателя, в эквивалентную ей работу (формулировка (1851г.) У. Томсона (лорда Кельвина));
– передача тепла от менее нагретого тела к более нагретому (формулировка (1850г.) Р.Ю.Э. Клаузиуса (1822–1888)).
Первое начало термодинамики часто формулируют как невозможность существования вечного двигателя I рода, который совершал бы работу, не черпая энергию из какого-либо источника.
Возможность использования энергии теплового движения частиц тела (теплового резервуара) для получения механической работы (без изменения состояния др. тел) означало бы возможность реализации так называемого вечного двигателя II рода, работа которого не противоречила бы закону сохранения энергии (т.е. I началу). Так, работа двигателя корабля за счёт охлаждения забортной воды океана – доступного и практически неисчерпаемого резервуара внутренней энергии – не противоречит закону сохранения энергии, но если, кроме охлаждения воды, нигде других изменений нет, то работа такого двигателя противоречит II началу термодинамики. В реальном тепловом двигателе процесс превращения теплоты в работу обязательно сопряжён с передачей определённого количества теплоты внешней среде. В результате тепловой резервуар двигателя охлаждается, а более холодная внешняя среда нагревается, что находится в согласии со вторым началом термодинамики, которое можно сформулировать и как невозможность существования вечного двигателя II рода (перпетуум мобиле II рода).
Второй закон термодинамики применим только к статистическим системам – коллективам, состоящим из большого числа частиц. К системам, состоящим из малого числа частиц, он неприменим. Если вернуться к уже рассмотренному выше примеру с шарами, то с уменьшением числа черных и белых шаров в опыте со встряхиванием, например, до 4 каждого цвета, возможны комбинации расположения шаров в рядах:
| Белые шары в нижнем/верхнем ряду, шт. | Число комбинаций, с помощью которых может быть получено данное состояние |
| 4/0 | |
| 3/1 | |
| 2/2 | |
| 1/3 | |
| 0/4 |
Равномерное, наиболее неупорядоченное распределение шаров уже не обладает подавляющим максимальным числом комбинаций реализации (и, следовательно, подавляюще большой вероятностью осуществления). Поэтому в таких системах возможны отклонения от равномерного распределения чего-либо, например, числа молекул газа в единице объема в двух соединенных трубкой сосудах (если молекул, например, четыре, то комбинация (2 – 2: два на два) может и не реализоваться). В этом случае говорят о флуктуациях величин, характеризующих состояние системы, – т.е. об их отклонении от некоторого среднего значения, соответствующего равномерному, наиболее неупорядоченному состоянию.
Дата добавления: 2015-05-05; просмотров: 1090;
