Закон сохранения механической энергии. Виды ударов.
При переходе системы из состояния 1 в состояние 2 справедливо:
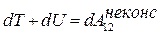. (3.10) – закон изменения механической энергии.
Если внешние неконсервативные силы отсутствуют, то
E=T+U=const. (3.11)
Формула (3.11) – закон сохранения механической энергии: в системе тел, на которые действуют только консервативные силы, полная механическая энергия сохраняется, то есть не изменяется со временем (нет ее диссипации, т.е. рассеяния).
При этом может возникнуть вопрос: "А как же быть с внешними консервативными силами?" Ответ: "Если внешние консервативные силы нескомпенсированы, то в систему включают тела, воздействующие этими силами, т.е. такие силы можно сделать «внутренними»".
Закон сохранения энергии является следствием фундаментального свойства времени – однородности. Однородность времени заключается в том, что физические законы инвариантны относительно выбора начала отсчета времени.
Удар абсолютно упругих и неупругих тел является ярким примером выполнения законов сохранения импульса и энергии. Под ударом (столкновением) в физике понимают взаимодействие тел при их сближении, которое длится очень короткое время, и условии, что на достаточно большом расстоянии тела можно рассматривать как свободные.
В механике рассматривают удары, предполагающие контакт между телами (удары бильярдных шаров, метеорита о землю, попадание пули в тележку с песком). УдарныеFудар dp/dt=Dp/Dt (или мгновенные (Dt~мкс)) силы взаимодействия между соударяющимися телами столь велики, что внешними силами можно пренебречь и считать для таких систем законы сохранения импульса и энергии выполненными. Тела во время удара испытывают деформации (упругие или неупругие). КЭ тел во время удара преобразуется в ПЭ упругого соударения, а затем частично или полностью вновь переходит в КЭ. Плоскость контакта называется плоскостью удара, а прямую, ей перпендикулярную и пересекающую ее в точке соприкосновения, называют линией удара. Если линия удара параллельна скоростям сталкивающихся тел, удар называется прямым; если эта линия проходит через центры сталкивающихся тел, удар называютцентральным. Скорость тел не достигает своего прежнего значения после удара.
Отношение нормальных составляющих скорости после и до удара называют коэффициентом восстановления (скорости): 
. Если e=0 – абсолютно неупругий удар (АНУ), e=1 – абсолютно упругий удар (АУУ). Для шаров из слоновой кости коэффициент e=0,89, из стали – e=0,56, а для свинцовых – e=0,01 т.е. для реальных тел 0<e<1.
Рассмотрим применение законов сохранения для прямого центрального удара двух шаров.
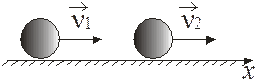
Рис. 3.5
Абсолютно упругий удар (АУУ). Пусть 
и 
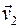– скорости тел до, а 
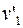и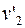 
– после удара (рис. 3.5). В случае, если скорость 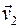направлена навстречу , в формулах ниже учитывают, что проекция скорости 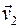будет равна 
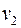и все рассуждения остаются верными.
Для АУУ выполняются законы сохранения импульса (так как импульс – векторная величина, то записан в проекции на ось Ох) и энергии:
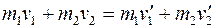. (3.13)
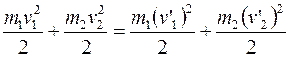, (3.14)
При анализе упругих столкновений удобно один из шаров представлять покоящимся (относительно шара m2 скорость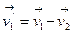 
).
Рассмотрим частный случай: АУУ – прямой центральный (лобовой) удар при n2=0. Тогда 
и 
:
а) m1=m2, тогда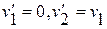 
(как бы «передача скорости»);
б) m1>m2, тогда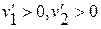 
(оба мяча движутся в направлении скорости первого мяча до удара);
в) m1<m2, тогда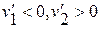 
(первый мяч отскочит от второго);
г) m1<<m2, тогда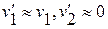 
(мячик отскочит от стены, см. рис. 3.6, 
)
Рис. 3.6
Абсолютно неупругий удар (АНУ). В этом случае тела объединяются и двигаются как одно целое.Потеря механической энергии при неупругом ударе происходит потому, что в этом случае помимо сил, пропорциональных деформациям, действуют силы, пропорциональные скорости – подобные силам сопротивления. При АНУ выполняется закон сохранения импульса и рассеивается часть КЭ DT:
,
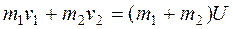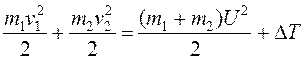. (3.17)
Тогда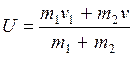 
и
.
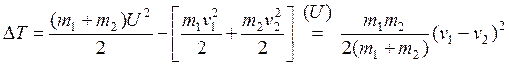Дата добавления: 2015-05-05; просмотров: 1569;