Энергия. Работа. Мощность. Кинетическая и потенциальная энергия.

В качестве единой количественной меры различных форм движения материи и соответствующих им взаимодействий в физике вводится скалярная величина – энергия.

В механике рассматривают механическую энергию (энергию механического движения и механических взаимодействий). Для количественного описания обмена энергии между телами используют понятие работа силы. Элементарной работой dA силы 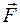на малом перемещении 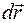точки О приложения силы называется скалярное произведение:

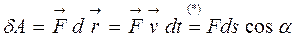, (3.1)

где 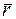– радиус-вектор точки О;

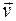– ее скорость;

dt – малый промежуток времени, в течение которого сила 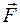совершает работу dA;

a – угол между направлением действия силы 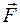и направлением перемещения 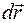(или ).

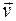Если угол a–острый, то dA>0 и сила ускоряющая, если угол a–тупой, то dA<0 и сила тормозящая (трения, например). Переход (*) в уравнение (3.1) справедлив в силу равенства 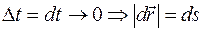. Из уравнения (3.1) следует, что сила не совершает работу, если точка приложения силы неподвижна ( 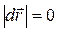) и если сила направлена перпендикулярно (по нормали) к траектории ( ).

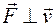Таким образом, работа силы на участке траекторий от точки 1 до точки 2 равна алгебраической сумме элементарных работ на отдельных, бесконечно малых участках:

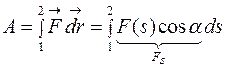. (3.2)

Геометрически работа – это площадь под кривой (рис. 3.1).

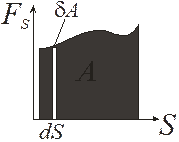
Рис. 3.1

Если 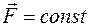, то 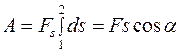. Сила называется потенциальной (консервативной), если ее работа зависит только от начального и конечного положений тела и не зависит от формы ее траектории. Для таких сил интеграл по замкнутому контуру L равен 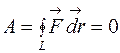. Для диссипативных сил работа зависит от формы траектории при перемещении тела (сила трения).

Чтобы охарактеризовать скорость совершения работы, вводят понятие мощности 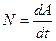. За время dt сила 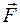совершает работу( 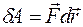) и мощность силы в данный момент (мгновенная мощность) равна 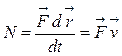. Единицы измерения: [A]=Дж; [N]=Ватт – Вт.

Кинетическая энергия(КЭ)системы – это энергия механического движения этой системы. Сила 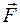, действующая на покоящееся тело и вызывающая его движение, совершает работу; энергия движущегося тела возрастает на величину затраченной работы. Таким образом, работа dA силы на пути, который тело проходит от нулевой скорости до скорости 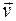, идет на увеличение КЭ тела Т:

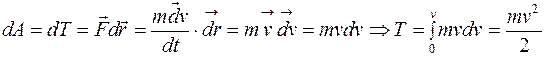. (3.3)

Кинетическая энергия Т является функцией состояния движения тела. Поскольку скорость 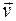зависит от выбора СО, КЭ тела в различных инерциальных системах отсчета (ИСО) имеет разные значения, определяемые согласно теореме Кёнига: КЭ системы материальных точек равна сумме КЭ всей массы системы, мысленно сосредоточенной в ее центре масс и движущейся вместе с ним, и КЭ той же системы в ее относительном движении по отношению к поступательно движущейся системе координат с началом в центре масс.

Потенциальная энергия (ПЭ) – это механическая энергия системы тел, определяемая их взаимным расположением и характером сил взаимодействия между ними.

Телу присуща потенциальная энергия U, если оно находится в поле потенциальных (консервативных) сил. Работа консервативных сил на элементарном перемещении равна приращению энергии U, взятому со знаком «–», так как работа совершается за счет убыли потенциальной энергии (зная U=f(r), можно определить модуль и направление силы F):

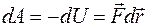, (3.4)

тогда 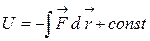, т.е. энергия U определяется с точностью до некоторой произвольной постоянной, но это не влияет на физические законы, так как в них, обычно, входят или разность энергий, или их производные по координатам. Нулевой уровень ПЭ выбирается произвольно из соображений удобства, поэтому может быть как больше, так и меньше нуля.

Конкретный вид функции U=f(r) зависит от характера силового поля. Так, тело, находящееся на высоте h<<R_Земли от поверхности земли в поле сил тяготения, обладает потенциальной энергией:

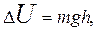(3.6)

Аналогично, при упругих деформациях, потенциальная энергия упруго–деформированного тела

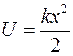. (3.7)

Потенциальная энергия системы является функцией ее состояния. Она зависит только от взаимного расположения тел (конфигурации) системы и от ее положения по отношению к внешним телам.

Полная энергия тела складывается из его кинетической и потенциальной энергий: E=T+U.