Решение задач линейного программирования
Для решения задач линейного программирования в MATLAB используется функция
linprog(f, a, b, ar, br, xmin, xmax),
где f - массив-столбец коэффициентов целевой функции, подлежащей минимизации;
а - матрица коэффициентов ограничений-неравенств, имеющих вид "меньше или равно" (коэффициенты каждого ограничения указываются в отдельной строке матрицы);
b - массив-столбец правых частей ограничений-неравенств;
аr - матрица коэффициентов ограничений-равенств (коэффициенты каждого ограничения указываются в отдельной строке матрицы);
br - массив-столбец правых частей ограничений-равенств;
xmin - массив-столбец ограничений на минимальные значения переменных;
хmах - массив-столбец ограничений на максимальные значения переменных.
Большой класс практических задач оптимизации может быть сведен к решению задачи линейного программирования.
Пример. Молочный завод выпускает два вида молочных продуктов (1) и (2), для чего используются два исходных вида сырья – А и B. Суточные запасы этих видов сырья составляют соответственно 6 и 8 т. Расходы сырья А и В на 1 т соответствующих продуктов приведены в таблице.
Таблица
| Исходный вид сырья | Расход исходных видов сырья ( в тоннах ) на тонну продуктов | Запас сырья, т | ||
| Продукт (1) | Продукт (2) | |||
| А | ||||
| В |
Изучение рынка сбыта показало, что суточный спрос на продукт (2) не превышает спроса на продукт (1) более чем на 1 т и, кроме того, не превышает 2 т. Прибыль от продукта (1) составляет 3000 ден.ед./т, от продукта (2) - 2000 ден.ед./т. Требуется определить, какое количество продуктов каждого вида следует производить, чтобы получить максимальную прибыль.
Построение математической модели задачи.
Обозначим через x1 и x2 ( т ) суточный обьем производства продуктов (1) и (2) соответственно.
Целевой функцией S является прибыль:
S = (3x1 + 2x2)1000 --> max (4)
Запишем условие задачи в виде системы ограничений:
1) ограничение по сырью А
x1 + 2x2 ≤ 6 (5)
2) ограничение по сырью В
2x1 + x2 ≤ 8 (6)
3) ограничения по спросу
x2 - x1 ≤ 1 (7)
x2 ≤ 2 ? (8)
Очевидно, должно также выполняться условие не отрицательности параметров
x1 ≥ 0 ; x2 ≥ 0. (9)
Как видно, рассматриваемая математическая модель записывается в форме общей задачи линейного программирования: найти значения оптимизируемых параметров x1 и x2, обеспечивающие максимум целевой функции (4) при ограничениях (5)...(8), а также при ограничениях на не отрицательность параметров (9).
Решение задачи в системе MatLab
Для решения задач линейного программирования применим процедуру linprog прикладного пакета Optimization Toolbox системы MatLab. Процедура имеет много вариантов обращения и может использовать различные алгоритмы.
Процедура решает задачу:
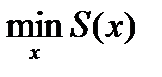
при ограничениях:
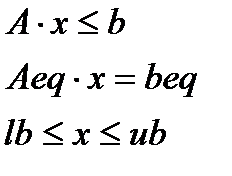
где S, x, b, beq, lb и ub – векторы, а A и Aeq – матрицы.
наиболее простая форма обращения:
x = linprog(S,A,b,Aeq,beq),
а наиболее полная:
[x,Sval,exitflag,output,lambda] = linprog(S,A,b,Aeq,beq,lb,ub,x0,options)
Для рассматриваемой задачи достаточно:
[x,Sval] = linprog(S,A,b,Aeq,beq,lb)
Здесь Sval – значение целевой функции.
Если необходимо найти максимум целевой функции, то ее коэффициенты следует взять с обратным знаком. Если в ограничениях неравенствах стоят знаки "≥", то знаки левых и правых частей неравенств следует взять с обратным знаком.
Рассмотренный пример может быть решен с помощью следующего сценария:
function optim
% ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
% ЦЕЛЕВАЯ ФУНКЦИЯ
% S = (3*X(1) + 2*X(2))*1000 -> max
% ОГРАНИЧЕНИЯ
% X(1) + 2*X(2) <= 6
% 2*X(1) + X(2) <= 8
% X(2) - X(1) <= 1
% X(2) <= 2
% X(1) >= 0; X(2) >= 0
%
S = [-3; -2];
A = [1 2
2 1
-1 1
0 1];
b = [6; 8; 1; 2];
lb = zeros(2,1); % ФОРМИРОВАНИЕ ВЕКТОРА [0; 0]
[x,Sval] = linprog(S,A,b,[],[],lb)
Результат будет в виде:
Optimization terminated successfully.
x =
3.3333
1.3333
Sval =
-12.6667
Таким образом, первый продукт должен производиться в объеме 3.3333т, а второй – 1.3333т. При этом прибыль составит 12.6667 тыс. ден. ед. и будет максимальной.
Дата добавления: 2015-04-03; просмотров: 4381;
