Метод ЭЙЛЕРА-КОШИ

В основе метода ломаных Эйлера лежит идея графического построения решения дифференциального уравнения, однако этот метод дает одновременно и способ нахождения искомой функции в численной (табличной) форме.

Пусть дано уравнение

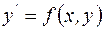(9)

с начальным условием

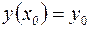. (10)

Выбрав достаточно малый шаг h, построим, начиная с точки х₀, систему равностоящих точек 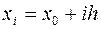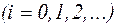. Вместо искомой

интегральной кривой на отрезке рассмотрим отрезок касательной к ней в точке 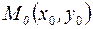(обозначим ее L₁) с уравнением

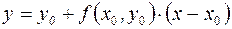При 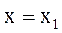из уравнения касательной получаем: 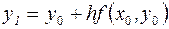, откуда видно, что приращение значения функции на первом шаге имеет вид: .

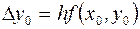Аналогично, проводя касательную 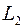некоторой интегральной кривой семейства в точке 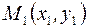, получим:

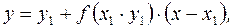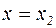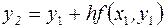что при дает т. е. 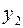получается из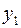

добавлением приращения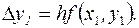

Таким образом, получение таблицы значений искомой функции 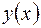по методу Эйлера заключается в циклическом применении пары формул:

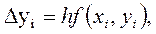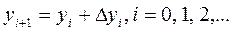(11)

Существуют различные уточнения метода Эйлера, повышающие его точность. Модификации метода обычно направлены на то, чтобы более точно определить направление перехода из точки 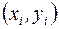точку . Метод Эйлера - Коши, например, рекомендует следующий порядок вычислений:

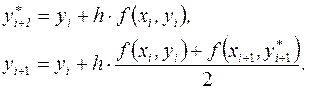(12)

Геометрически это означает, что мы определяем направление интегральной кривой в исходной точке 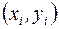и во вспомогательной точке 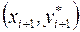, а в качестве окончательного берем среднее этих направлений.

В соответствии с методом Эйлера – Коши запишем итерационные уравнения нахождения значения скорости n_i+1 в следующий момент времени из предыдущего n_i (обозначим t – шаг по времени).Обозначив

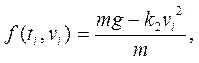(13)

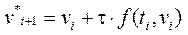Тогда в момент времени t_i+1 согласно методу Эйлера – Коши запишем формулы:

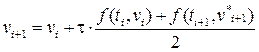(14)

Тогда, подставляя (13) в формулы (14), в итоге получим:

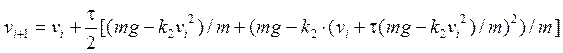
Для ускорения процесса работы над задачей целесообразно вместо составления программы воспользоваться готовой прикладной программой (например, табличным процессором Excel).

В Excel в ячейках D2, D4, D6, D8 таблицы будем хранить соответственно значения шага вычислений t, массы «безпарашютиста» m, величины mg, коэффициента 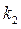. Это связано с тем, что все константы удобно хранить в отдельных ячейках, чтобы в случае их изменения не пришлось переписывать расчетные формулы Тогда для вычисления значения 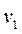в ячейке В4 нужно записать формулу:

=B3+$D$2/2*(($D$6-$D$8*B3^2)/$D$4+($D$6-

$D$8*(B3+$D$2*($D$6-$D$8*B3^2)/$D$4)^2)/$D$4)

и произвести автозаполнение столбца В.

В столбце А в ячейку А4 нужно записать формулу: =СУММ(А3;$D$2) и произвести автозаполнение столбца А.