Свободное падение тела.

Математическая модель свободного падения тела – уравнение второго закона Ньютона с учетом двух сил, действующих на тело – силы тяжести и силы сопротивления среды : 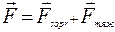, где , .

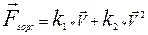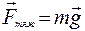Движение является одномерным. Проецируя силу 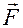, скорость 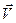и перемещение 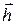на ось, направленную вертикально вниз, из (3) получаем

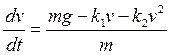
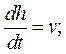(7)

В конкретных задачах можно одной из составляющих силы сопротивления пренебречь (если она заведомо много меньше другой).

Если скорость движения мала (v = 0.1 м/с), т. е. k₂ v² << k_1×v, то отбрасывается квадратичная составляющая скорости в формуле силы сопротивления.

Если скорость движения велика (v =100 м/с),т. е. k₂ v² >> k _1×v, то отбрасывается линейная составляющая скорости в формуле силы сопротивления.

Частичное тестирование моделирующей программы можно провести для движения без сопротивления. Аналитическое решение в этом случае общеизвестно.

Входные параметры модели:

· Начальная высота тела;

· Начальная скорость тела;

· Величины, определяющие коэффициенты сопротивления среды .

Задача

Парашютист совершает затяжной прыжок. Считая массу парашютиста заданной (m=80 кг), определить, начиная с какого времени после начала полета скорость человека - «безпарашютиста» становится постоянной. Построить график зависимости скорости падения «безпарашютиста» от времени.

Решение.

Нужно определить характер изменения скорости со временем, если все параметры, входящие в уравнения системы (7), заданы. При такой постановке модель носит дескриптивный характер. Ясно, что при наличии сопротивления, растущего со скоростью, в какой-то момент сила сопротивления сравняется с силой тяжести, после чего скорость больше возрастать не будет. Выберем путь численного моделирования. Итак, математическая модель выражается системой дифференциальных уравнений (7), однако, поскольку нужен график изменения скорости, то будем рассматривать только второе уравнение системы (7).

Поставим вопрос: влияет ли на полет «безпарашютиста» линейная составляющая скорости в ?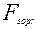

Скорость движения достаточно большая,поэтому вкладом линейной составляющей силы сопротивления k_1×v можно пренебречь. Тогда получим систему дифференциальных уравнений:

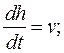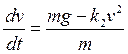(8)

;

из которых будем рассматривать только второе уравнение. Здесь v –скорость, t – время, h – высота, m – масса, g – ускорение свободного падения, k₂ – коэффициент квадратичной составляющей скорости.

Вычислим значение коэффициента k₂ для данной задачи. Средний рост человека возьмем средний - 1,7 м, а полуобхват грудной клетки –характерный размер – это приблизительно 0,4 м. Выберем число с = 1,22 как среднее между коэффициентами для диска и для полусферы (выбор для качественной оценки правдоподобен). Оценим площадь поперечного сечения:

S = 1,7×0,4=0,7 м².

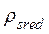= 1,29 кг/м³

Тогда 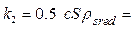0,5×1,22×0,7×1,29 = 0.55083 кг/м.

Масса парашютиста m = 80 кг.

Теперь можно приступить к численному решению задачи. При этом следует воспользоваться одним из известных численных методов интегрирования систем обыкновенных дифференциальных уравнений. Решение находится с помощью, так называемого, исправленного метода Эйлера – метода Эйлера - Коши.