Идеальная гибкая обратная связь.
В качестве корректирующего звена выберем идеальное дифференцирующее звено.
.
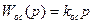Пусть охваченное звено имеет:
,
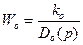тогда:
. (8.12)
Гибкая обратная связь не влияет на коэффициент передачи охватываемого звена и изменяет коэффициент при р в знаменателе передаточной функции W.
Рассмотрим пример 1:
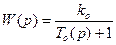
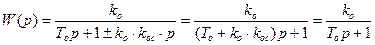
где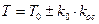 
.
Постоянная времени Т изменилась на ko×koc.
При отрицательной обратной связи Т увеличивается.
При положительной обратной связи Т уменьшается.
Таким образом, гибкая обратная связь изменяет быстродействие без изменения коэффициента передачи звена.
В звене второго порядка гибкая обратная связь сильно уменьшает коэффициент передачи.
Положительная гибкая обратная связь форсирует переходный процесс, как при возрастании, так и при снижении выходного сигнала САР.
Рассмотрим пример 2:
Охват дифференцирующей связью с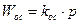 
интегрирующего звена с 
.
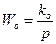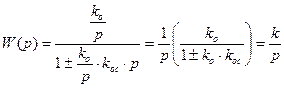, (8.13)
где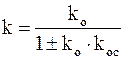 
.
Гибкая обратная связь изменяет коэффициент передачи, не меняя типа звена.
Дата добавления: 2015-04-25; просмотров: 975;