Коррекция с помощью интегрирующих звеньев.

Применение интегрирующих звеньев для коррекции динамических свойств системы при последовательном включении их в прямую цепь обусловлено возможностью без уменьшения запаса устойчивости и практически без заметного изменения частоты среза поднять коэффициент усиления на низких частотах и тем самым существенно уменьшить ошибки в установившемся режиме.

Передаточная функция приведенной на рисунке RC – цепи (рисунок 8.3):

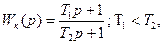(8.5)

где T₁=R₂C₂; T₂=(R₁+R₂)C₂.

АФХ – где K=1 имеет форму полуокружности 1.

Из графика видно (рисунок 8.4), что интегральная цепь вносит отставание по фазе, которое максимально на частоте 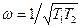и равно Q_m. Сравнение характеристики 1 с идеальной характеристикой 2, соответствует звену с передаточной функцией:

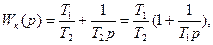(8.6)

показывает, что в области высоких частот имеется наибольшее сближение.

ЛАХ наглядно показывает, что контур уменьшает усиление на высоких частотах. Следовательно, при компенсации этого ослабления в системе будет достигнуто увеличение коэффициента усиления на низких частотах.

Рассмотрим это на предыдущем примере.

Нескорректированная система имеет ЛАХ (рисунок 8.9) – кривые 1, 2, 3 и ФЧХ – кривая 1. При частоте среза w_с имеем g₁. Для увеличения коэффициента усиления на низких частотах без существенного уменьшения запаса устойчивости по фазе необходимо, чтобы частота сопряжения v=1/T₁, определяемая наименьшей из постоянных времени контура, была ниже частоты среза на 2-3 октавы. С учетом этого строим ЛАХ корректирующего звена (4-5-6-7), в результате получили ЛАХ скорректированного контура (1-8-9-10-11). Компенсируя ослабление увеличения на высоких частотах получили ЛАХ (12-13-14-2-3). Заштрихованная область указывает на увеличение K_ус в области низких частот. Это достигнуто без существенного изменения запаса устойчивости по фазе и частоты среза. Увеличение коэффициента усиления на низких частотах уменьшает ошибки в установившемся режиме и тем самым повышает статическую точность системы.

Вывод: при коррекции с помощью интегрирующих устройств система в меньшей мере подвержена влиянию помех.