Тема 11. Выборочное наблюдение

Выборочное наблюдение – вид не сплошного наблюдения, при котором из общей (генеральной совокупности) отбирается посредством метода случайного отбора некоторая часть, называемая выборочной совокупностью, обобщающие показатели, характеризующие эту часть совокупности, распространяются на всю совокупность.

Применение выборочного метода связано с возникновением ошибок репрезентативности, которые представляют собой разность между обобщающими показателями генеральной выборочной совокупностей.

Выборочная совокупность может формироваться разными методами. Может иметь место индивидуальный отбор (когда отбирается каждый раз одна единица совокупности) или серийный (отбор производится сериями, гнездами, упаковками и т.п. и в них обследуются все единицы).

После обследования отобранные единицы могут быть возвращены в генеральную совокупность, где имеют одинаковую со всеми единицами вероятность вновь попасть в выборку – повторный отбор, либо могут не участвовать в дальнейшем оборе – бесповторный отбор.

Отбор может быть произведен собственно-случайным способом, механическим и типическим.

При собственно-случайной выборке отбор производится жеребьевкой.

Механический способ отбора используется в тех случаях, когда имеется возможность составить список единиц совокупности в порядке их естественного расположения (по алфавиту, по времени появлении и т.п.). отбор осуществляется механически – через определенный интервал.

При типическом отборе обследуемая генеральная совокупность подразделяется на типические группы, из которых затем отбирается определенное число единиц так, чтобы сохранить в выборе структуру генеральной совокупности.

Ошибки репрезентативности могут быть рассчитаны как средняя или стандартная (μ) и максимальная с определенной вероятностью – предельная ( ).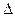

Средняя ошибка выборки для собственно случайного и механического способа.

При повторном методе отбора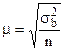

При бесповторном методе отбора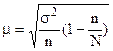

где 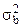- дисперсия выборочных данных; n – объем выборки; N – объем генеральной совокупности.

Средняя ошибка типического отбора.

При повторном методе отбора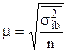

При бесповторном методе отбора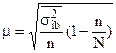

где 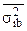- средняя из групповых вариаций в выборке по типическим группам.

Средняя ошибка при отборе сериями (серийная выборка).

При повторном отборе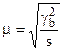

При бесповторном отборе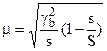

где 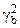- межгрупповая вариация; s – количество отобранных серий; S – количество серий в генеральной совокупности.

Предельная ошибка выборки ( 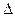) связана со средней ошибкой и коэффициентом доверия (t).

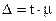
Коэффициент доверия зависит от вероятности, с которой можно гарантировать определенные размеры предельной ошибки:

Обобщающая характеристика в генеральной совокупности ( 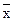) определяется доверительным интервалом, уточнение обобщающей характеристики выборочной совокупности ( 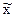) на предельную ошибку выборки:

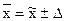или 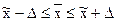с заданной вероятностью.

Приведенные выше формулы ошибок выборки позволяют заранее рассчитать тот объем выборки (репрезентативная выборка), при котором отклонение выборочных показателей от генеральных не превысит заданных размеров, гарантируемых с определенной вероятностью.

Репрезентативная выборка (n).

При повторном отборе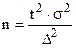

При бесповторном отборе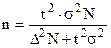

При определении необходимой численности выборки, для определения дисперсии используют данные предыдущих обследований. При полном отсутствии каких-либо данных о вариации задают максимальную величину дисперсии: для количественного признака.

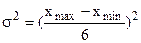
Для альтернативного признака .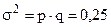

Малой выборкой называют выборку, объем которой не превышает 20 единиц ( ).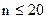

Средняя ошибка малой выборки ( 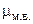) определяется по формуле:

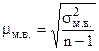
Для увязки средней и предельной ошибок малой выборки используется коэффициент распределения Стьюдента (псевдоним В. Гссета).

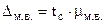
где 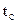- коэффициент Стьюдента, определяемый по распределению Стьюдента 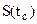в зависимости от n.

Вероятность того, что характеристика генеральной совокупности не выйдет за пределы 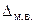, с распределением Стьюдента связана следующим образом:

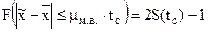
последняя формула применяется для нахождения пределов генеральной средней с заданной вероятностью.