Экономических рисков

Экономические явления и процессы связаны со случайными величинами. Случайной называют величину, которая может принять одно из возможных значений, наперед неизвестное и зависящее от случайных причин, которые невозможно учесть. Например, из предназначенных для продажи 50 изделий – количество проданных изделий – случайная величина, имеющая одно из значений: 0, 1, 2, 3, … 50.

Случайная величина может быть дискретной и непрерывной. Дискретные случайные величины, в отличие от непрерывных изменяются скачкообразно.

Перечень всех возможных значений дискретной случайной величины и их вероятностей называется Законом распределения дискретной случайной величины.

Сумма вероятностей всех случайных дискретных величин должна равняться единице.

Наиболее вероятное ожидаемое значение случайной величины представляет собой математическое ожидание ( ).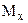

Математическое ожидание дискретной случайной величины равно сумме произведений всех ее возможных значений на их вероятности:

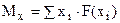
где 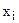- i – вариант возможного значения случайной величины x; i – порядковый номер возможного варианта значения случайной величины x; F(x_i) – вероятность i-го варианта значения случайной величины x.

С увеличением числа вариантов случайной дискретной величины математическое ожидание может быть определено как среднее арифметическое полученных значений, то есть;

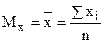
где n – количество вариантов случайной величины.

Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от математического ожидания.

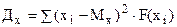
где Д_х – дисперсия дискретной случайной величины.

По результатам большого числа измерений (большое количество вариантов случайной дискретной величины) дисперсия может определяться по формуле:

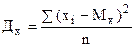
Стандартное отклонение случайной величины ( 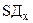) характеризует ее изменчивость и служит для построения характеристик, распределяющих меру риска принятия решений, основанных на информации о случайных величинах.

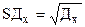
Относительная мера риска (R_x) оценивается коэффициентом вариации:

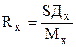
Непрерывная случайная величина может принимать все значения из определенного диапазона. Число возможных значений непрерывной случайной величины бесконечно велико.

Закон распределения непрерывных случайных величин в экономических системах чаще всего может иметь форму нормального распределения.

Функции случайных величин – это функции, значения которых являются случайные величины. Для оценки ожидаемых результатов и рисков достаточно определить их числовые характеристики: М_х, Д_х, SД_х, R_x.

Если функция может быть задана аналитически, то ее числовые характеристики могут быть легко определены по значениям числовых характеристик входящих в ее состав случайных величин.

Если аргументы функции – случайные независимые величины, то характеристики функций определяются математическим ожиданием и дисперсией ее аргументов с учетом правил:

1) Математическое ожидание суммы случайных независимых величин (независимых аргументов) 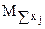сумме их математических ожиданий .

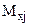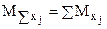
где j – количество независимых аргументов; 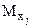- математическое ожидание каждого независимого аргумента.

2) Дисперсия суммы случайных независимых величин 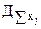равна сумме их дисперсий .

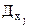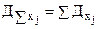
3) Математическое ожидание произведения случайных независимых величин равно произведению их математических ожиданий.

4) Дисперсия произведения случайных независимых величин равна произведению их дисперсий.