Тема 9. Динамические ряды распределения

Динамические ряды распределения представляют собой ряды изменяющихся во времени значений признака (уровней ряда) расположенных в хронологическом порядке.

В зависимости от способа выражения уровней (у) ряды динамики подразделяются на ряды абсолютных, относительных и средних величин.

Динамические ряды могут быть интервальными, если характеристика явления дается за определенный промежуток времени (день, месяц, год и т.п.) и моментными, если составляющее его показатели определяются на определенный момент времени рассматриваемого периода.

В зависимости от расстояния между уровнями, ряды динамики подразделяются на равномерные (представлены всеми последующими периодами) и неравномерные.

При построении рядов динамики необходимо обеспечить сопоставимость уровней ряда динамики, это означает условия, по которому уровни ряда должны быть исчислены по одной методике и пределах одинаковых территориальных границ.

Средний уровень ряда определяется:

в моментном ряду (равномерном) по формуле средней хронологической простой

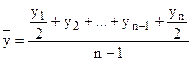
в моментном (неравномерном ряду) по формуле средней хронологической взвешенной

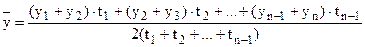
в интервальном равномерном

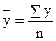
в интервальном неравномерном

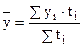
Аналитические показатели ряда динамки представляют собой результат сравнений двух уровней ряда динамки. Сравнение может осуществляться базисным (каждый последующий уровень сравнивается с первым, принятым за базу) и цепным способами (каждый последующий уровень сравнивается с предыдущим).

Абсолютный прирост показывает на сколько абсолютных единиц один уровень ряда динамики больше или меньше другого:

абсолютный прирост базисный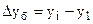

абсолютный прирост цепной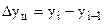

Средний абсолютный прирост определяется только для цепных показателей ( ).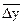

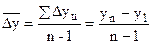
Темп роста – показывает во сколько раз один уровень ряда динамики больше или меньше другого.

Темп роста базисный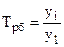

Темп роста цепной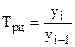

Средний темп роста ( )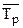

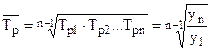
Темп прироста показывает на сколько процентов один уровень больше или меньше другого уровня.

Темп прироста базисный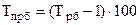

Темп прироста цепной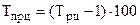

Средний темп прироста ( )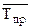

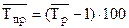
Абсолютное значение одного процента прироста (А) представляет собой отношение абсолютного прироста к темпу прироста и определяется по формуле: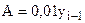

Абсолютное значение одного процента прироста определяется только для цепных проростов. Среднее абсолютное значение одного процента прироста не рассчитывается.

Важнейшей задачей характеристики динамики общественных явлений является выявление основной тенденции развития.

Эта задача решается методами выравнивания рядов динамики, которые включают механическое выравнивание, метод скользящей средней, аналитическое выравнивание.

Механическое выравнивание – заключается в укрупнении интервалов и определении для укрупненного интервала среднего или суммарного значения признака.

Метод скользящей средней заключается в последовательном расчете средних уровней из заданного числа по порядку уровней ряда, каждый раз отбрасывая один уровень в начале и добавляя один следующий.

Каждое звено скользящей средней – это уровень за соответствующий период, который относится к середине выбранного периода, если число уровней скольжения нечетное. например для ряда динамики, представленного уровнями у₁ у₂ у₃ у₄ у₅ скольжение 3-х уровневой средней будет иметь вид:

; ; .

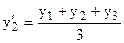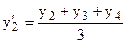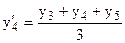Нахождение скользящей средней по четному числу уровней несколько сложнее, так как средняя может быть отнесена к середине между двумя периодами, находящимся в середине интервала сглаживания.

Чтобы ликвидировать такой сдвиг, применяют способ центрирования. Центрирование заключается в нахождении средней из двух смежных скользящих средних для отнесения полученного уровня к определенному периоду.

;

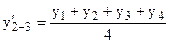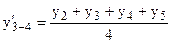
Центрированием получаем .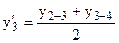

Аналитическое выравнивание предполагает представление уровней данного ряда динамики в виде функции времени 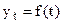, называемой адекватной формулой ряда динамики или аналитическое выражение тренда.

Адекватная формула развития может быть представлена прямолинейной зависимостью 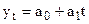для выражения равномерного роста (снижения); и криволинейными зависимостями типа гиперболы, параболы, степенной функции для выражения замедленного или ускоренного роста (снижения).

Проблема аналитического выравнивания сводится к определению параметров адекватной формулы развития аналогично методике определения параметров уравнения регрессии (см. тему 8), с применением упрощенного расчета на основе переноса начала координат в середину ряда динамики, получая, таким образом, .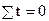

В этом случае система нормальных уравнений для нахождения параметров прямой будет иметь вид.

; ;

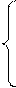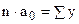
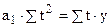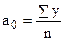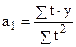
для параболы 2^го порядка

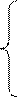
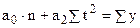
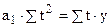
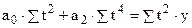
Нумерация последовательности периодов времени при нечетном числе уровней 1, 2, 3, …, n после переноса начала координат t будет …-3, -2, -1, 0, 1, 2, 3, … при четном числе уровней … -5, -3, -1, 1, 3, 5 …

Статистическое прогнозирование динамики социально-экономических явлений основывается на предположении, что закономерность развития, действующая в прошлом (внутри ряда динамики), сохраняется и в прошлом и будущем, т.е. прогноз основан на экстраполяции.

Экстраполяция, проводимая в будущее, называется перспективной; в прошлое – ретроспективной.

Методы экстраполяции включают в себя: метод среднего абсолютного прироста, метод среднего темпа роста, метод использования адекватной формулы развития.

Прогнозирование по среднему абсолютному приросту может быть выполнено в том случае, если тенденция может быть представлена равномерным ростом (снижением).

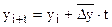
Прогнозирование по среднему темпу роста можно осуществлять в случае, когда есть основание считать, что общая тенденция ряда характеризуется показательной (экспотенциальной) кривой.

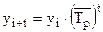
где t – срок прогноза.

Наиболее распространенным методом прогнозирования является аналитическое выражение тренда. При этом для выхода за границы исследуемого периода достаточно продолжить значения независимой переменной времени (t). Используя адекватную формулу ряда динамики.

Для оценки адекватности аналитического выражения тренда может использоваться показатель средней ошибки аппроксимации ( ).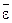

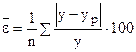
где 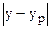- линейные отклонения абсолютных величин эмпирических и выровненных точек регрессии. Если 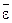≤10 %, то вероятность прогноза велика.

При анализе рядов динамики иногда приходится прибегать к определению некоторых неизвестных уровней внутри данного ряда динамики, то есть к интерполяции.

Интерполяция основана на тех же методах, что и экстраполяция.

При исследовании месячных данных многих явлений может иметь место определенные повторяющиеся колебания, которые существенно не изменяются за длительный период времени. Они являются результатом влияния природно-климатических условий, общих экономических факторов, а также прочих факторов, которые могут быть регулируемы.

В статистике, периодические колебания, которые имеют определенный и постоянный период внутри годового промежутка называются сезонными колебаниями или сезонными волнами.

Сезонные колебания характеризуются показателями, называемыми индексами сезонности (У_с).

Индексом сезонности называют процентное отношение среднемесячного (за три года) уровня к среднегодовому уровню.

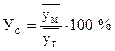
степень сезонности оценивают на основании среднеквадратического отклонения индексов сезонности от 100 %.

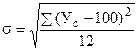
Во многих рядах динамики может наблюдаться определенная зависимость уровней последующих периодов от предшествующих им.

Зависимость между последовательными уровнями ряда динамики называется автокорреляцией.

Автокорреляцию оценивают при помощи коэффициента автокорреляции (r_a).

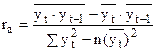
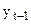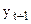Для расчета коэффициента автокорреляции параллельно с исходными уровнями ряда (у_t) записывают уровни, сдвинутые на один период, т.е. (или ), при этом чтобы сдвинутый ряд не укорачивался, его можно условно дополнить принимая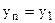

Исходный ряд динамики: …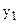

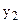
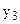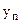
Сдвинутый ряд динамики …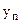

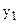
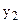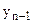
Коэффициент автокорреляции может рассчитываться не только между соседними уровнями (сдвинутыми на один период), но и сдвинутыми на любое число единиц времени. Этот сдвиг именуется временным лагом.

Для рядов динамики, у которых установлено наличие автокорреляции ( 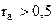), каждый уровень ( 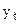) может рассматриваться как функция предыдущих значений уровней.

Уравнение, выражающее эту зависимость, называется уравнением авторегрессии. Уравнение авторегрессии, связывающее исходные уровни ряда с теми же уровнями, сдвинутыми на определенный лаг(m), т.е. 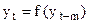, находится по общим правилам регрессионного анализа.