Тема 7. Теоретические кривые распределения
Графически вариационные ряды распределения можно представить в виде полигона распределения (для дискретного ряда) или в виде гистограммы (для интервального ряда), как это показано на рис. 2,3.

Рис. 2. Полигон распределения
 |
Рис. 3. Гистограмма
По форме полигона распределения или гистограмме можно сделать вывод о форме распределения. Однако судить о закономерностях данного эмпирического распределения по полигону или гистограмме рискованно, так как оно зависит в частности, от числа исследуемых единиц.
Характерные черты распределения проявляются при увеличении числа наблюдений.
Предел, в виде сплошной плавной линии, к которому стремится гистограмма, при уменьшении величины интервала или полигон при увеличении числа наблюдений именуется кривой распределения.
Среди различных кривых распределения особой место занимает нормальное распределение.
Нормальное распределение представляет собой симметричную колоколообразную кривую, имеющую максимум в точке, соответствующей 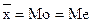 , рис. 4.
, рис. 4.
 |
- σ + σ
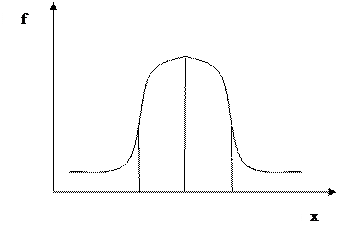
Рис. 4. Кривая нормального распределения
Основными свойствами кривой нормального распределения являются:
1) 68,3 % всей площади, ограниченной осью х и кривой нормального распределения сосредоточено на участке 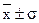 ;
;
2) 95,4 % площади на участке 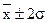 ;
;
3) 99,7 % площади на 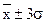 ;
;
4) Точки перегиба кривой нормального распределения находятся на расстоянии 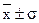 .
.
На практике эмпирическое распределение может отличаться от нормального имея ассиметрию или эксцесс.
Степень ассиметрии оценивается в помощью нормированного момента третьего порядка.
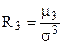
где 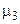 - центральный момент третьего порядка.
- центральный момент третьего порядка.
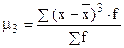

Если R3>0,5 независимо от знака, ассиметрия считается существенной. Знак указывает на направленность ассиметрии «+» - правосторонняя, «-» левосторонняя.
При соблюдении условия 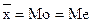 ряд распределения может быть островершинным или низковершинным.
ряд распределения может быть островершинным или низковершинным.
Показатель эксцесса отражает эту особенность.
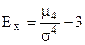
где 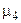 - центральный момент четвертого порядка.
- центральный момент четвертого порядка.

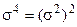
Если Ех>0, то распределение островершинно, если Ех<0 –низковершинно.
Для определения теоретических частот распределения в случае близости к нормальному распределению может использоваться уравнение.
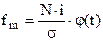
где 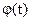 - табулируемая величина, отыскиваемая по нормированным отклонениям каждого варианта признака (t)
- табулируемая величина, отыскиваемая по нормированным отклонениям каждого варианта признака (t) 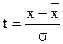 ; i – величина интервала; N – количество единиц совокупности.
; i – величина интервала; N – количество единиц совокупности.
Если имеет место существенная ассиметрия или аксцесс, то распределение Шарлье:
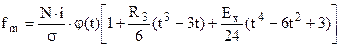
Вычисление теоретических частот производится исходя из той или иной гипотезы о предполагаемом законе распределения. Гипотеза о том, насколько приятое теоретическое распределение соответствует данному эмпирическому проверяется с использованием критерия Пирсона «хи-квадрат» (χ2).
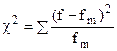
где f, fm – соответственно эмпирические и теоретические частоты.
Для оценки степени соответствия эмпирических и теоретических распределений по данному критерию используются специальные таблицы.
В случае отсутствия специальных таблиц, критерий «хи-квадрат» можно оценить критерием В.И. Романовского (Кр):
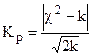
где k – число степеней свободы.
Для нормального распределения, распределения Шарлье 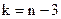 , где n – число интервалов (групп).
, где n – число интервалов (групп).
Расхождение между эмпирическими и теоретическими частотами считаются случайными, если значение 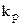 меньше 3.
меньше 3.
Дата добавления: 2015-04-19; просмотров: 1074;
