Тема 6. Показатели вариации

Средние величины, характеризуя вариационный ряд одним числом, не учитывают степень вариации признака.

Для ее измерения используют показатели вариации: размах вариации, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение, коэффициент вариации.

Размах вариации (R)

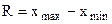
Среднее линейное отклонение (Д) представляет собой среднюю арифметическую из абсолютных значений отклонений вариантов от средней.

Рассчитывают:

простое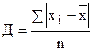

взвешенное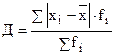

Дисперсия ( 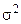) наиболее часто используемый показатель вариации, показывает среднюю площадь отклонений вариантов признака от средней величины.

простая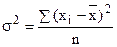

взвешенная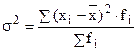

Преобразовав указанные формулы определения дисперсии можно получить упрощенный вариант формулы (дисперсия методом моментов).

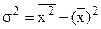
Среднее квадратическое отклонение ( 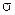) определяется как квадратный корень из дисперсии.

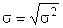
Достоинство среднего квадратического отклонения по сравнению со средним линейным отклонением в том, что при его вычислении никакого условного допущения о необходимости суммирования отклонений вариантов от средней без учета их знаков не делается.

Для сравнения степени вариации признака в разных совокупностях используется коэффициент вариации (ν):

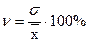
Коэффициент вариации может, также, использоваться для характеристики степени однородности исследуемой совокупности. Вариация признака определяется не только для количественных, но и для качественных признаков, представленных альтернативным признаком:

Дисперсия альтернативного признака равна

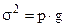
где p – доля единиц совокупности обладающих данными признаком; g – доля единиц совокупности не обладающих данным признаком. p+g=1.

В аналитической группировки для изучения вариации результативного признака определяются следующие виды дисперсий:

Внутригрупповая дисперсия ( 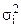) показывает вариацию результативного признака в каждой группе, выделенной по факторному признаку:

где х – варианты результативного признака; 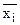- среднее значение признака по группе факторного признака; - частота признака в каждой группе.

Межгрупповая дисперсия ( 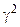) показывает вариацию групповых средних ( 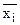) от средней по всей совокупности ( ).

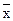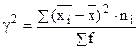
где 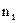- количество единиц в каждой группе.

Общая дисперсия ( 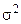) показывает вариацию во всей совокупности без учета выделения групп по факторному признаку.

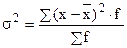
Между общей дисперсией ( 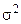), средней из групповых ( 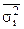) и межгрупповой дисперсией ( 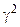) существует взаимосвязь, называемая «правило сложения дисперсий».

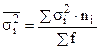
С использованием указанных дисперсий можно определить влияние факторного (группировочного) признака на вариацию результативного.

Оценка влияния основывается на расчете коэффициента детерминации или эмпирического корреляционного отношения (η).

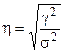
Если η>0,5 это свидетельствует о большом влиянии факторного признака на вариацию результативного признака.