Законы постоянного тока
Сопротивление проводника. Закон Ома в интегральной форме.
 |
Рассмотрим отрезок однородного цилиндрического проводника длиной l. Для того, чтобы в этом проводнике протекал постоянный ток I, необходимо внутри проводника поддерживать постоянное электрическое поле, напряженностью Е. Обозначим φ1 и φ2 – электрические потенциалы в начальном и конечном сечении проводника, тогда
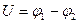- падение потенциала на участке АВ, называемое напряжением, приложенным к проводнику (рис.11.2).
Экспериментально было установлено, что при изменении напряжении меняется и ток, текущий в проводнике, т.е.
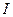~U.
Обозначим коэффициент пропорциональности, характеризующий электрическую проводимость проводника через G. Тогда, величина R, обратная проводимости проводника называется его электрическим сопротивлением.
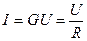(11.2.1)
Уравнение (11.2.1) называется законом Ома в интегральной форме: ток, идущий в проводнике, численно равен отношению приложенного напряжения к сопротивлению проводника.
В системе СИ единицей сопротивления является Ом: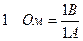 
– это сопротивление такого проводника, в котором при напряжении 1 В идет ток в 1 А.
Сопротивление проводника зависит от его геометрических размеров и формы, а также материала, из которого сделан проводник.
Для цилиндрических проводников
,
где ρ – удельное сопротивление вещества, из которого сделан проводник, т.е. сопротивление проводника в форме куба с ребром 1 м при силе тока текущему параллельно одному из ребер куба.
 |
Сопротивление проводника зависит от внешних условий (температуры и давления). Экспериментально было доказано, что сопротивление проводника линейно возрастает с температурой по закону:
где α – температурный коэффициент сопротивления, t – температура проводника, R0 – сопротивление проводника при температуре 0°С.
Закон Ома в дифференциальной форме
 |
Рассмотрим отрезок однородного цилиндрического проводника длиной dl и площадью поперечного сечения dS (рис.11.3).
Согласно закону Ома (11.2.1)
(11.2.2)
Учитывая, что сопротивление проводника зависит от его геометрических размеров
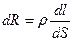, (11.2.4)
 |
Подставляя уравнение (11.2.4) в (11.2.3) получим:
По определению, плотность тока
Следовательно, с учетом формулы (10.8.4), получим
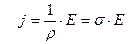(11.2.5)
Уравнение (11.2.5) носит название закона Ома в дифференциальной форме. Этот закон показывает условие создание поля внутри проводника, где имеет место, направленное движение заряженных частиц. Одновременно зарождается поле плотности тока, величина которого существенно зависит от взаимодействия свободных носителей тока в проводнике с элементами среды.
Закон Ома для замкнутой цепи. ЭДС.
Рассмотрим участок цепи (рис.11.4). На электрические заряды действуют сторонние силы Fстор, перемещающие эти заряды против электрического поля.
 |
Выделим малый элемент тока длиной dl, так, чтобы площадь поперечного сечения S на этом участке можно было считать постоянным.
Для участка цепи, в котором действуют сторонние силы уравнение (11.2.5) примет вид:
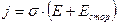
или с учетом формулы (11.1.2)
(11.2.6)
Умножим уравнение (11.2.6) на выражение 
:
.
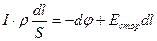Проинтегрируем полученное уравнение:
учитывая, что
получим
.
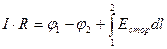Выражение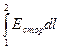 
=ε называется электродвижущей силой (ЭДС) источника тока, включенного на этом участке. Этот интеграл численно равен работе, совершаемой сторонними силами при переносе заряда по цепи.
Тогда
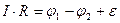(11.2.7)
 |
Выражение (11.2.7) носит название закона Ома для участка цепи, содержащей источник тока.
Рассмотрим внешнюю цепь (рис.11.5), замкнутую на источник тока с ЭДС и внутренним сопротивлением r.
Полное сопротивление всей цепи равно сумме сопротивлений источника (внутреннее) и потребителя (внешнее):
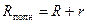
Для замкнутой цепи потенциалы точек равны, т.е.
.
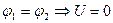Тогда уравнение (11.2.7) примет вид:
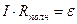
Или
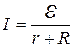(11.2.8)
Выражение (11.2.8) носит название закона Ома для замкнутой цепи.
Дата добавления: 2015-04-19; просмотров: 856;