Магнитное поле и его характеристики
В 19 веке опытным путем были исследованы законы взаимодействия постоянных магнитов и проводников, по которым пропускался электрический ток. Опыты показали, что подобно тому, как в пространстве, окружающем электрические заряды, возникает электростатическое поле, так и в пространстве, окружающем токи и постоянные магниты, возникает силовое поле, которое называется магнитным.
Были установлены два экспериментальных факта:
1) магнитное поле действует на движущиеся заряды;
2) движущиеся заряды создают магнитное поле.
Этим магнитное поле существенно отличается от электростатического, которое действует как на движущие, так и на покоящиеся заряды. Магнитное поле не действует на покоящиеся заряды. Опыт показывает, что характер воздействия магнитного поля на ток зависит от формы проводника, по которому течет ток; от расположения проводника и от направления тока.
Сила взаимодействия, приходящая на единицу длины каждого из параллельных проводников, пропорциональна величинам токов в них и обратно пропорциональна расстоянию между ними:
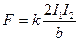 ,
,
где 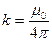 - коэффициент пропорциональности, µ0=4π·10-7 Гн/м – магнитная постоянная, b – расстояние между проводниками.
- коэффициент пропорциональности, µ0=4π·10-7 Гн/м – магнитная постоянная, b – расстояние между проводниками.
Основной характеристикой магнитного поля определяют силу действия со стороны поля на единичный проводник с током, и называется магнитной индукцией B.
Магнитная индукцияв данной точке однородного магнитного поля определяется максимальным вращающим моментом, действующим на рамку с магнитным моментом, равным единице, когда нормаль к рамке перпендикулярна направлению поля:
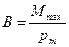 . .
| (12.1.1) |
Магнитное поле в отличие от электрического, не оказывает действия на покоящийся заряд, т.е. магнитное поле порождается движущимися зарядами. Еще одной характеристикой магнитного поля является напряженность Н.
Магнитная индукция B связана с напряженностью H магнитного поля соотношением
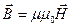 , ,
| (12.1.2) |
где μ – относительная магнитная проницаемость среды.
Опыт показывает, что для магнитного поля, как и для электрического справедлив принцип суперпозиции: магнитная индукция 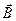 результирующего поля, порождаемое несколькими движущимися зарядами (токами), равно векторной сумме магнитных индукций
результирующего поля, порождаемое несколькими движущимися зарядами (токами), равно векторной сумме магнитных индукций 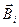 , создаваемых каждым зарядом (током) в отдельности:
, создаваемых каждым зарядом (током) в отдельности:
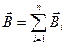 .
.
Если величина и направление вектора магнитной индукции во всех точках некоторой области пространства одинаковы, то поле называется однородным.
 |
Для графического изображения магнитного поля вводят понятие силовых линий вектора магнитной индукции (рис.12.1), которые проводят таким образом, что касательная к каждой точке пространства совпадает с вектором магнитной индукции в данной точке. Густота линий определяется модулем магнитной индукции.
 |
Рассмотрим магнитное поле, создаваемое в некоторой точке Р точечным зарядом q, движущимся с постоянной скоростью v (рис.12.2).
Экспериментально было показано, что при скоростях намного меньше скорости света v << c магнитная индукция поля движущегося заряда определяется формулой:
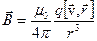 ,
,
или в скалярной форме
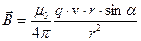 . (12.1.3)
. (12.1.3)
Из формулы (12.1.3) следует, что вектор магнитной индукции в каждой точке Р направлен к плоскости, проходящей через направление вектора v и Р.
Единицей измерения магнитной индукции в системе СИ называется Тесла (Тл).
Рассмотрим малый элемент провода длины dl (рис.12.3.). Введем вектор 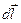 , направленный по оси элемента тока, в сторону, в которую течет ток.
, направленный по оси элемента тока, в сторону, в которую течет ток.
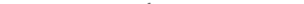 |
В 1820 году тремя французскими учеными Био, Саваром и Лапласом была получена эмпирическая формула, определяющая вектор магнитной индукции от проводника с током:
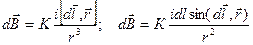 (12.1.4)
(12.1.4)
где 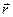 – радиус – вектор, проведенный из элемента тока в рассматриваемую точку поля, K – коэффициент пропорциональности
– радиус – вектор, проведенный из элемента тока в рассматриваемую точку поля, K – коэффициент пропорциональности
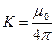 ,
,
где 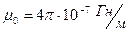 - магнитная постоянная.
- магнитная постоянная.
Из закона Био—Савара—Лапласа следует, что вектор магнитной индукции В в какой-либо точке С магнитного поля перпендикулярен плоскости, в которой лежат векторы dl и 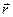 , и его направление таково, что из конца вектора dB поворот вектора dl до совмещения с вектором г по кратчайшему пути виден происходящим против часовой стрелки (рис.12.3).
, и его направление таково, что из конца вектора dB поворот вектора dl до совмещения с вектором г по кратчайшему пути виден происходящим против часовой стрелки (рис.12.3).
С помощью закона Био-Савара – Лапласа, применяя принцип суперпозиции, можно вычислить магнитное поле любых систем токов.
Расчет магнитного поля для прямого тока.
 |
Полем прямого тока называется поле, созданное током, текущим по тонкому прямому проводнику бесконечной длины. Вычислим напряженность поля в точке М, находящийся на расстоянии R от этого проводника. Для этого выделим бесконечно малый элемент тока dl. (рис. 12.4)
Определим направление вектора магнитной индукции элемента тока dB в точке М. По правилу буравчика вектор dB направлен перпендикулярно к плоскости, проходящей через элемент тока и точку, в которой вычисляется поле.
По закону Био-Савара-Лапласа, модуль вектора магнитной индукции элемента тока
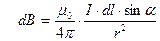 , (12.1.5)
, (12.1.5)
где α – угол между векторами dl и r.
Из рисунка
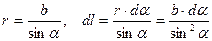 (12.1.6)
(12.1.6)
Тогда закон Био-Савара-Лапласа примет вид
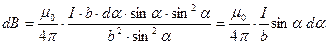
Магнитная индукция всего проводника будет равна алгебраической сумме модулей векторов магнитной индукции или
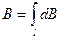
Угол α для каждого элемента бесконечно прямого тока изменяется в пределах от 0 до π. Следовательно,
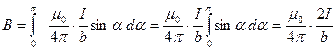 - магнитная индукция поля прямого тока.
- магнитная индукция поля прямого тока.
Линии магнитной индукции поля прямого тока представляют собой систему охватывающих провод концентрических окружностей.
Магнитное поле действует не только на проводники с током, но и на отдельные электрические заряды, движущиеся в поле.
На заряд, движущийся в магнитном поле, действует сила, которую называется магнитной. Эта сила определяется зарядом q, скоростью его движения υ и магнитной индукцией В, в той точке, где находится заряд в рассматриваемый момент времени и называется силой Лоренца. Опытным путем установлено, что сила F, действующая на заряд, движущийся в магнитном поле, определяется формулой
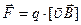
модуль силы Лоренца
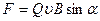 , ,
| (12.1.7) |
где 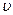 – скорость движения зарядов, α – угол между векторами
– скорость движения зарядов, α – угол между векторами 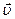 и
и 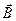 .
.
Сила Лоренца всегда направлена перпендикулярно скорости заряженной частицы, сообщая ей нормальное ускорение. Следовательно, сила Лоренца не совершает работы. Она изменяет только направление скорости движения частицы в магнитном поле. Модуль скорости заряда и его кинетическая энергия при движении в магнитном поле не изменяются.
Дата добавления: 2015-04-19; просмотров: 1088;
