Потенциал. Разность потенциалов. Потенциал поля точечного заряда и системы точечных зарядов.
Энергетической характеристикой поля в данной точке является потенциал. Потенциал численно равен потенциальной энергии, которой обладает в данной точке единичный заряд
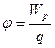 . .
| (10.5.1) |
Потенциал поля точечного заряда Q, находящегося в точке на расстоянии r от него равен
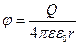 . .
| (10.5.2) |
Если поле образовано несколькими точечными зарядами, то потенциал результирующего поля
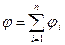 , ,
| (10.5.3) |
где 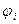 - потенциал поля, создаваемого отдельным зарядом.
- потенциал поля, создаваемого отдельным зарядом.
работа сил поля над зарядом может быть представлена через разность потенциалов
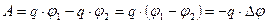
| (10.5.4) |
где Δφ – разность потенциалов между двумя точками электрического поля. Таким образом, потенциал электрического поля численно измеряется работой, совершаемой полем при перемещении единичного положительного пробного заряда по любому пути из данной точки.
В системе Си разность потенциалов измеряется в вольтах (В).
Для графического изображения распределения потенциала в электростатическом поле пользуются системой так называемых поверхностей равного потенциала (Эквипотенциальных поверхностей). Эквипотенциальные поверхности обычно проводят так, чтобы разности потенциалов между двумя соседними эквипотенциальными поверхностями были одинаковы. Тогда густота эквипотенциальных поверхностей наглядно характеризует напряженность поля в разных точках. Там, где эти поверхности расположены гуще, напряженность поля больше.
На рисунке 10.9. пунктиром изображены силовые линии, сплошными линиями - сечения эквипотенциальных поверхностей для: положительного точечного заряда (а), диполя (б), двух одноименных зарядов (в), заряженного металлического проводника сложной конфигурации (г).
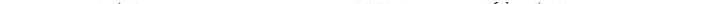 |
Для точечного заряда эквипотенциальные поверхности -концентрические сферы. С другой стороны, линии напряженности - радиальные прямые. Следовательно, линии напряженности перпендикулярны эквипотенциальным поверхностям. Во всех случаях вектор Е перпендикулярен эквипотенциальным поверхностям и всегда направлен в сторону убывания потенциала.
Дата добавления: 2015-04-19; просмотров: 1463;
