Проводники в электростатическом поле. Электроемкость.
В металлических проводниках концентрация свободных электронов достаточно высока, порядка 1028 м-3. Если проводник поместить в электростатическое поле, то произойдет перераспределение свободных электронов, часть из них будет находиться на поверхности проводника, создавая поле, напряженность которого противоположна напряженности внешнего электростатического поля, установится равновесное состояние (электростатическое равновесие). При равновесии не будет направленного движения электронов, а это означает отсутствие результирующего электрического поля внутри проводника, в противном случае свободные заряды постоянно направленно перемещались бы под действием поля, что противоречит закону сохранения энергии. Так как напряженность поля в проводнике равна нулю, то через любую замкнутую поверхность внутри проводника поток вектора Е равен нулю. Как следует из теоремы Гаусса (10.7.6), алгебраическая сумма электрических зарядов внутри такой поверхности равна нулю. Таким образом, несмотря на перераспределение зарядов, концентрация электронов равна концентрации положительных ионов. Поэтому удаление внутренней части металлического проводника не должно повлиять на размещение зарядов на его поверхности [рис. 10.15; в одинаковых электрических полях расположены одинаковые по форме проводники, но один из них сплошной (а), а другой — полый (б)].
 |
Из формулы (10.6.1) следует, что потенциал всего проводника одинаков, а его поверхность является эквипотенциальной. Следовательно, силовые линии нормальны поверхности проводника (см., например, рис. 10.15).
Таким образом, проводник экранирует внутреннее пространство от внешних электростатических полей. Эту особенность проводников используют при электростатической защите. Например, при соответствующих измерениях или для безопасности приборы, людей, животных помещают внутрь металлических проводящих систем, обычно выполненных в виде сетки.
Если источник электрического поля — заряд — находится внутри проводника, то проводник уже не будет экраном, а станет источником электрического поля во внешнем пространстве.
Соединение проводником какого-либо тела с землей называют заземлением. При заземлении заряженных проводников, в том числе и тела человека, они теряют заряд и их потенциал будет равен потенциалу земли. Заземление корпусов приборов и аппаратов способствует их безопасной эксплуатации, так как исключает возможность для персонала оказаться под напряжением корпуса аппарата и земли.
Между зарядом и потенциалом проводника существует определенная взаимосвязь. Коэффициент пропорциональности между ними носит название электроемкости. Электроемкость проводника численно равна величине заряда, который нужно сообщить данному проводнику для увеличения его потенциала на единицу:
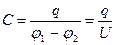
| (10.8.1) |
Единицей емкости является фарад (1Ф)– емкость такого уединенного проводника,потенциал которогоповышается на 1В при сообщении заряда 1Кл:
1Ф= 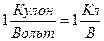
На практике применяется также единицы емкости: 10-6 фарад = 1 мкФ (микрофарад), 10-12 фарад = 1 пкФ (пикофарад). Величину емкости любого проводника легко определить, деля величину заряда проводника на его потенциал. Так металлический шар радиуса R, несущий заряд Q, имеет потенциал
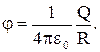
| (10.8.2) |
Следовательно, его емкость С равна
| С = 4pe0R. | (10.8.3) |
 |
Для практических целей используется система из двух противоположно заряженных пластин (обкладки), называемая конденсатором. Геометрически это может быть плоская, цилиндрическая или шаровая конфигурация.
Самый простой случай – это плоский конденсатор, который состоит из двух проводящих плоских пластин, пространство между которыми заполнено диэлектриком с проницаемостью ε (рис.10.16.,а). Напряженность поля между пластинами конденсатора
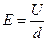
| (10.8.4) |
где U – разность потенциалов между пластинами конденсатора, d – расстояние между ними.
Если на единице поверхности имеется заряд 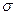 и диэлектриком является вакуум, то емкость плоского конденсатора С равна
и диэлектриком является вакуум, то емкость плоского конденсатора С равна
С = 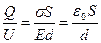 , ,
| (10.8.5) |
где d – расстояние между обкладками конденсатора, S – площадь обкладок конденсатора.
Если диэлектриком является не вакуум, а вещество с диэлектрической проницаемостью 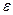 , заполняющее все пространство, где имеется электрическое поле (пространство между обкладками), то емкость конденсатора
, заполняющее все пространство, где имеется электрическое поле (пространство между обкладками), то емкость конденсатора
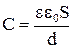 . .
| (10.8.6) |
Известны и другие формы конденсаторов. Так, например, цилиндрические обкладки, разделенные слоем стекла, образуют так называемую лейденскую банку. В экспериментах по наблюдению фотоэффекта часто используется сферический конденсатор(рис.10.16, в), емкость которого
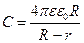 , ,
| (10.8.7) |
где R – радиус внешней сферы, r – радиус внутренней сферы. В частном случае, когда внешний радиус R гораздо больше внутреннего r, то емкость сферического конденсатора определяется по следующей формуле:
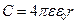 , ,
| (10.8.8) |
Емкость цилиндрического конденсатора (рис.10.16, б), состоящего из двух коаксиальных цилиндров длиной L и радиусами r (внутренний) и R (внешний) определяется
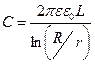 , ,
| (10.8.9) |
Если напряжение на конденсаторе сделать слишком большим, то конденсатор «пробивается», т.е. между его обкладками возникает искра (внутри диэлектрика или по его поверхности) и конденсатор портится вследствие нарушения изоляции. Поэтому каждый конденсатор характеризуется не только своей емкостью, но еще и максимальным рабочим напряжением.
Для того чтобы, располагая определенными конденсаторами, осуществить желаемую емкость при нужном рабочем напряжении, конденсаторы соединяются в батареи.
 |
На рис. 10.17. показаны соединения конденсаторов.
При параллельном соединении конденсаторов заряды на всех пластинах складываются и складываются емкости, тогда как потенциалы всех пластин одинакового знака оказываются одинаковыми:
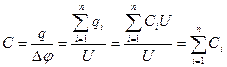 ; ;
| (10.8.10) |
для последовательного соединения конденсаторовобщее напряжение
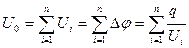
т.к. заряды на всех конденсаторах одинаковы (q=const).
Учитывая, что 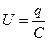 , получим
, получим
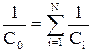
| (10.8.11) |
В частности, для двух последовательно соединенных конденсаторов общая емкость определяется как:
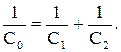
| (10.8.12) |
Заряженный конденсатор обладает определенной энергией. Энергия электрического поля конденсатора
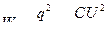 . .
| (10.8.13) |
В однородном поле плоского конденсатора его энергия W должна быть распределена равномерно по всему объему поля V, поэтому используют объемную плотность энергии w, т.е. энергия единицы объема поля, определяемая соотношением
w= 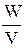 = = 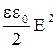 . .
| (10.8.14) |
Дата добавления: 2015-04-19; просмотров: 1521;
