Циркуляция вектора напряженности. Физический смысл. Понятие потока. Теорема Гаусса.
Определим работу по перемещению заряда q под действием силы Кулона из одной точки эквипотенциальной поверхности в другую.
где φ1 и φ2 – потенциалы точек. Из определения эквипотенциальных поверхностей следует, что φ1 = φ2, тогда
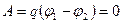
Таким образом,
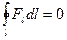(10.7.1)
т.е. работа по перемещению любого объекта по замкнутому пути равна нулю.
Учитывая, что
→ 
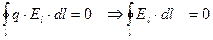(10.7.2)
Этот интеграл называется циркуляцией напряженности вдоль замкнутого контура. Силовое поле, которое удовлетворяет этому условию, является потенциальным (например, электростатическое поле).
Физическим смыслом циркуляции вектора напряженности является работа по перемещению единичного заряда по замкнутому контуру.
 |
Введем понятие потока вектора электрической напряженности. Для этого рассмотрим в электрическом поле плоскую поверхность S (рис.10.10). Будем считать сначала, что поле однородно. Пустьn–единичная нормаль к площадке dS (достаточно малой, чтобы пренебречь изменением электрической напряженности Е в пределах площадки). Поток dФэ электрической напряженности через эту площадку определяется как произведение нормальной компоненты Е и dS.
Тогда величину
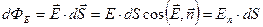(10.7.3)
называют потоком вектора электрической напряженности через данную поверхность.
Если электрическое поле неоднородно, то полный поток вектора электрической напряженности через данную поверхность
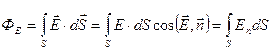(10.7.4)
Например, для электростатического поля точечного заряда поток вектора напряженности:
,
где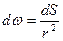 
- телесный угол.
Определим физический смысл потока. Согласно правилу проведения линий вектора напряженности, величина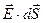 
, численно равна количеству силовых линий вектора напряженности, пронизывающих площадку, т.е.
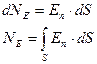(10.7.5)
Определим поток электростатического поля, пронизывающий сферу радиусом R (рис.10.11).
 |
заряд q, расположенный в центре сферы создает электрическое поле напряженностью:
Так как радиус сферы постоянен (R=const), то модуль напряженности на всей сфере одинаков и равен
 |
Направление вектора напряженности
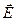в каждой точке совпадает с направлением внешней нормали 
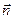к сфере, т.е.
Тогда
Если внутри замкнутой поверхности находятся N точечных зарядов q1, q2, …, qn, то по принципу наложения полей напряженность результирующего поля:
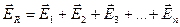
Поэтому
(10.7.6)
Уравнение (10.7.6) носит название теоремы Гаусса: поток вектора напряженности электрического поля в вакууме сквозь замкнутую поверхность произвольной формы равен отношению алгебраической суммы зарядов, находящейся внутри этой поверхности, к электрической постоянной.
Расчет напряженности электростатического поля бесконечной равномерно заряженной плоскости при помощи теоремы Гаусса.
 |
Представим себе равномерно заряженную бесконечную плоскость с постоянной поверхностной плотностью заряда σ (рис.10.12).
Построим бесконечно узкий прямой цилиндр, пересекающий данную плоскость, основания которого параллельны заряженной плоскости и лежат по разные стороны от нее на одинаковых расстояниях.
Поток смещения сквозь замкнутую цилиндрическую поверхность:
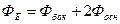
Так как образующие цилиндра параллельны линиям напряженности, то поток вектора напряженности через боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равен сумме потоков сквозь его основания:
 |
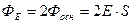
По теореме Гаусса
Следовательно
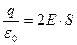
Заряд связан с поверхностной плотностью:
.
Если пластина помещена в какую-либо диэлектрическую среду, то напряженность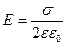 
.
Дата добавления: 2015-04-19; просмотров: 1568;