Вихревое электрическое поле. Ток смещения
Из закона индукции Фарадея следует, что изменение сцепленного с замкнутым проводом потока Фм магнитной индукции приводит к возникновению э.д.с. в неподвижном контуре, т. е. в нем возникают сторонние силы не электростатического происхождения, действующие на покоящиеся заряды. Дж. К. Максвелл высказал гипотезу, что всякое переменное магнитное поле возбуждает в окружающем пространстве электрическое поле, которое служит причиной возникновения индукционного тока в контуре. При этом контур, в котором появляется э.д.с., является всего лишь «индикатором» наличия этого поля. Обозначим это поле ЕВ, тогда закон электромагнитной индукции для неподвижного контура L означает следующее
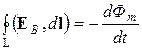. (14.3.1)
Подставим в эту формулу выражение для магнитного потока и поменяем порядок интегрирования по площади и дифференцирования по времени, тогда
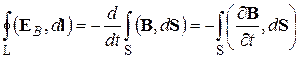. (14.3.2.)
Здесь символ частной производной фактически означает, что интеграл берется по неподвижной поверхности S, в точках которой B=B(x,y,z,t) меняется со временем. В отличие от электрического поля неподвижных зарядов электрическое поле, возбужденное магнитным полем, как и само магнитное поле, является вихревым, т. е. имеет не нулевую циркуляцию по замкнутому контуру.
 |
Для установления количественной взаимосвязи между меняющимся электрическим полем и возбуждаемым за счет этого магнитным полем Максвелл ввел в рассмотрение так называемый ток смещения Iсм. Согласно теории Максвелла в цепи переменного тока, содержащей, например, заряжающийся и разряжающийся конденсатор (рис.14.5.), переменное электрическое поле создает такое магнитное поле, как если бы между обкладками проходил ток Iсм, равный току проводимости I в подводящих проводах.
Выразим ток смещения через характеристики поля между пластинами, считая поле между пластинами однородным.
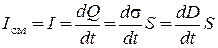. (14.3.3)
Здесь Q – заряд на пластинах, s – поверхностная плотность заряда на пластинах, D – модуль электрической индукции (электрического смещения) между пластинами. Напомним, что для плоского конденсатора D = e0eE =s. Из (14.3.3) следует, что производная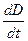 
имеет размерность плотности тока (А/м2).
Максвелл ввел величину
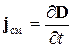, (14.3.4)
которую назвал плотностью тока смещения, и дал следующее определение для тока смещения. Ток смещения через поверхность S равен потоку вектора jсм через эту поверхность:
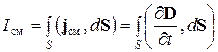. (14.3.5)
Максвелл предположил, что токи смещения наравне с обычными токами проводимости играют существенную роль в создании магнитного поля. Используя введенное им понятие плотности полного тока
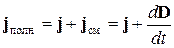, (14.3.6)
Максвелл обобщил теорему о циркуляции магнитной напряженности на случай нестационарных токов:
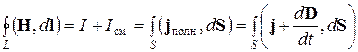. (14.3.7.)
Правильность этого соотношения была подтверждена последующими экспериментами, в частности экспериментами Г. Герца по изучению электромагнитных волн, существование которых были теоретически предсказано Максвеллом.
Дата добавления: 2015-04-19; просмотров: 1848;