Механические гармонические колебания

Пусть материальная точка совершает гармонические колебания вдоль горизонтальной оси координат х около положения равновесия принятого за начало координат.

Силы, неупругие по природе, но аналогичные по свойствам силам, возникающим при малых деформациях упругих тел, называют квазиупругими.

Зависимость координаты х от времени будет задаваться уравнением

x = A cos (wt+j₀).

По второму закону Ньютона сила, действующая на колеблющуюся материальную точку массой т определяется по уравнению

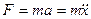
Найдем вторую производную по времени от уравнения гармонических колебаний:

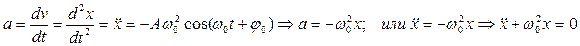
Данное уравнение называется дифференциальным уравнением свободных незатухающих колебаний. Решением дифференциального уравнения является выражение:

x = A cos (wt+j₀).

Следовательно, сила пропорциональна смещению материальной точки из положения равновесия и направлена в сторону положения равновесия, т.е.

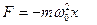
Найдем кинетическую энергию системы, колеблющейся по закону

x = A cos wt ,

приняв, что начальная фаза j₀=0. Скорость равна первой производной по времени от смещения, т.е.

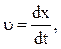
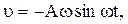
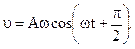
Кинетическая энергия может быть записана в виде

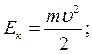
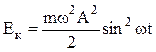
или .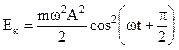

Известно, что

.

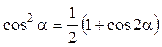Поэтому выражение для кинетической энергии можно переписать в виде

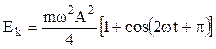. (15.2.1)

Таким образом, кинетическая энергия меняется со временем также по гармоническому закону, но по сравнению с координатой x с удвоенной частотой.

При вычислении потенциальной энергии квазиупругих и упругих сил условимся отсчитывать её от положения равновесия, т.е. положим, что при x=0, E_р=0.

Тогда потенциальная энергия в точке x будет численно равна работе квазиупругой силы, совершенной при перемещении из положения равновесия в данную точку и взятой с обратным знаком

.

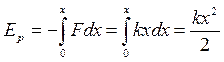Учитывая, что x = A cos wt и k=mw² получим

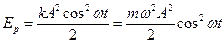. (15.2.2)

Используя формулу преобразования 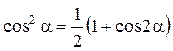, получим следующее выражение для потенциальной энергии:

.

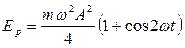Следовательно, потенциальная энергия также меняется со временем по гармоническому закону, но по сравнению с координатой x с удвоенной частотой и со сдвигом фазы относительно кинетической энергии Е_к на p.

Найдем полную энергию системы, совершающей гармоническое колебательное движение с частотой w и амплитудой А:

;

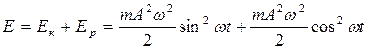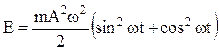
или

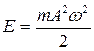. (15.2.3)

Таким образом, полная энергия гармонически колеблющейся системы есть величина постоянная и пропорциональная квадрату амплитуды колебаний.

В процессе движения происходит непрерывный переход кинетической энергии в потенциальную и обратно, но сумма их остается постоянной. Когда система проходит через положение равновесия x=0, потенциальная энергия обращается в нуль, а кинетическая энергия максимальна и равна полной энергии, т.е.

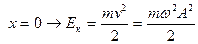
Когда колеблющаяся система доходит до одного из крайних положений x=±A, то u=0 и кинетическая энергия обращается в нуль

,

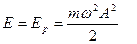
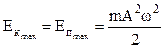т.е. потенциальная энергия максимальна и равна полной энергии.