Уравнение Бернулли. Одно из важнейших уравнений гидромеханики было получено в 1738 году швейцарским учёным Даниилом Бернулли

Одно из важнейших уравнений гидромеханики было получено в 1738 году швейцарским учёным Даниилом Бернулли. Ему впервые удалось описать движение несжимаемой идеальной жидкости (силы трения между элементами идеальной жидкости, а также между идеальной жидкостью и стенками сосуда отсутствуют). Уравнение Бернулли имеет вид:

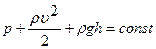(5.4.1)

где р – давление жидкости, ρ – её плотность, υ – скорость движения, g – ускорение свободного падения, h – высота, на которой находится элемент жидкости.

Согласно уравнению Бернулли, в случае установившегося течения, для которого не имеют существенного значения все другие характеристики текущей среды, кроме плотности (удельного веса), полный напор одинаков во всех поперечных сечениях трубки тока.

Слагаемые, входящие в уравнение Бернулли, имеют размерность и смысл давления. Давление р называют статическим; оно не связано с движением жидкости и может быть измерено, например, манометром, перемещающимся вместе с жидкостью. Давление 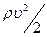называют динамическим; оно обусловлено движением жидкости и проявляется при ее торможении. Сумма статического и динамического давлений есть полное давление жидкости:

.

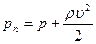Давление 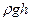- гидростатическое. В состоянии невесомости гидростатического давление отсутствует, с увеличением перегрузок оно возрастает. Используя эту терминологию уравнение Бернулли можно сформулировать как закон: в различных точках линии тока идеальной жидкости сумма статического, динамического и гидростатического давлений одинакова.

Выделим мысленно в жидко­сти трубку тока, сечениями ко­торой являются открытая по­верхность жидкости S₁ и сече­ние струи при выходе из отвер­стия S₂ (если не принять спе­циальных мер, то сечение струи будет меньше отвер­стия). Для всех точек каждого из этих сечений скорость жид­кости υ и высоту h над некото­рым исходным уровнем можно считать одинаковыми. Поэтому к данным сечениям можно применить теорему Бернулли. Давления р₁ и р₂ в обоих сечениях одинаковы и равны атмосферному. Скоростью υ₁ пе­ремещения открытой поверх­ности жидкости ввиду ее малости можно пренебречь. Поэтому уравнение Бернулли в данном случае упро­щается следующим образом:

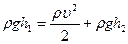(5.4.2)

где υ— скорость жидкости в сечении S₂ (скорость истечения из отверстия). Сократив на ρ, можно на­писать,

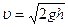(5.4.3)

где h = h₁ — h₂ — высота открытой поверхности над отверстием.

Формула (5.4.3) называется формулой Торричелли. Из нее следует, что скорость истечения жидкости из отверстия, находящегося на глубине h под открытой поверхностью жидкости, совпадет со скоростью, которую приобретает любое тело, падая с высоты h (в случае, если сопротивлением воздуха можно пренебречь). Этот результат получен в пред­положении, что жидкость идеальна. Для реальных жидкостей скорость истечения будет меньше, причем тем сильнее отличается от значения, определяемого формулой Торричелли, чем больше внутреннее трение в жидкости. Например, глицерин будет вытекать из сосуда медленнее, чем вода.

Если к отверстию в стенке трубы присоединить манометрическую трубку, то жидкость в такой трубке поднимется на высоту, равную гидростатическому напору. Трубка, имеющая одновременно торцевое и боковые манометрические отверстия, называется трубкой Пито и используется для определения скорости течения по измеренному скоростному напору. Трубки Пито входят в комплект измерительного оборудования всех самолетов, а также широко применяются для измерений скорости течения в трубопроводах, вентиляционных воздуховодах, в аэро- и гидродинамических трубах.

Если скорость течения равна нулю (т.е. среда не движется), то уравнение Бернулли сводится к простому уравнению гидростатики.

В тех случаях, когда скорость течения отлична от нуля, уравнение Бернулли совместно с уравнениями неразрывности и закона сохранения количества движения позволяет решать практически важные задачи – о расходе среды, текущей через измерительные диафрагмы, поверх измерительных и водосбросных водосливов и под затворы шлюзовых галерей; о траектории струи жидкости; о форме, скорости и силе волн, действующих на суда и волноломы. Хотя в таких задачах обычно рассматривается течение воды под атмосферным слоем воздуха, аналогичные процессы гравитационного характера имеют место в случае течения более холодной (и, следовательно, более плотной) воды под более теплой, как и других жидкостей и газов разной плотности. Таким образом, водным потокам в реках аналогичны океанские течения и ветры, поскольку все гравитационные явления подчиняются одним и тем же законам гидроаэромеханики.