Резонанс токов

Резонанс при параллельном соединении индуктивности и емкости, при взаимной компенсации реактивных составляющих токов в параллельных ветвях, называют резонансом токов.

Если к цепи, изображенной на рис. 5-1, приложено переменное синусоидальное напряжение

U_вх=√2U_вхsinωt, (5.2)

то ток равен

i_вх = √2U_вх√g²+ σ²∙sin(ωt±φ) = √2I_вх sin(ωt±φ), (5.3)

где

φ = arctg σ/g; g = R/( R²+( ωL)²); σ = σ_L – σ_C = ωL/(R²+( ωL)²) – ωC

Из приведенного выражения видно, что ток будет совпадать с приложенным напряжением при условии σ = 0 или

ωL/(R²+( ωL)²) – ωC = 0, т.е. σ_L = σ_C (5.4)

Таким образом, при резонансе токов входная реактивная проводимость цепи 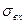равна нулю, а полная проводимость 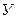имеет наименьшее значение, поэтому ток в неразветвленной части цепи минимален.

При резонансе токов в параллельных ветвях реактивные составляющие токов равны между собой:

.

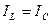и могут во много раз превышать ток в неразветвленной части цепи, что характеризуется величиной добротности :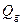

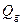= I_C/I_вх = I_L/I_вх = ρ/R = (1–200) (5.5)

ρ = √ L/C. (5.6)

где 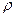- волновое или характеристическое сопротивление контура.

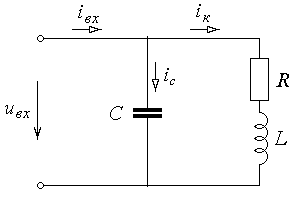
Рис. 5-1. Схема замещения параллельной цепи

Векторная диаграмма резонанса токов в цепи (рис. 5-1) имеет вид:

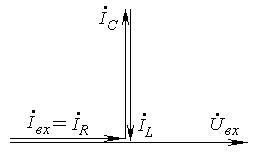
Рис. 5-2. Векторная диаграмма резонанса токов