Нерезонансные режимы

Режимы вне резонанса можно получить, если вывести систему из резонанса, т.е. нарушить условие (5.1), изменяя собственную частоту контура с помощью индуктивности 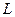при постоянной емкости 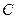, или изменяя емкость 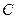при постоянной индуктивности 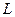. В результате этой операции можно получить частотные характеристики (рис. 5-3 и рис. 5-4).

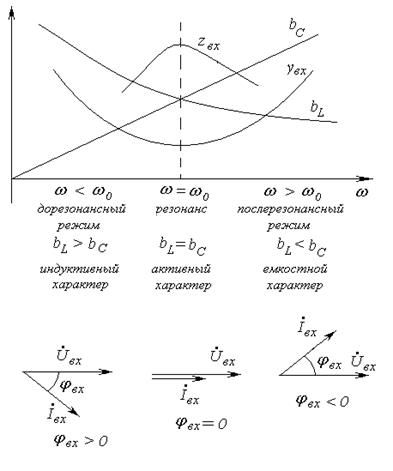
Рис. 5-3. Частотные характеристики проводимостей и входного сопротивления параллельной цепи

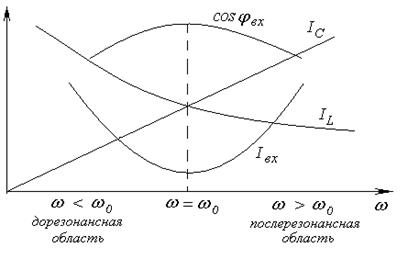
Рис. 5-4. Частотные характеристики токов и коэффициента мощности параллельной цепи

Следует отметить, что частотные характеристики параллельной цепи обратны по отношению к частотным характеристикам последовательной цепи, это происходит по-тому, что параллельное соединение элементов является обратным последовательному соединению. Острота частотных характеристик зависят от добротности цепи Q_g. Чем выше значение добротности, тем более острыми получаются пики кривых и лучше избирательные свойства цепи.

Изменяя величину емкости конденсатора при постоянной индуктивности можно получить графики функциональных зависимостей в параллельной цепи (рис. 5-5) и построить соответствующие векторные диаграммы (рис. 5-6).

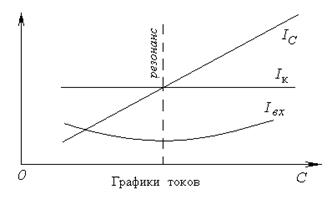
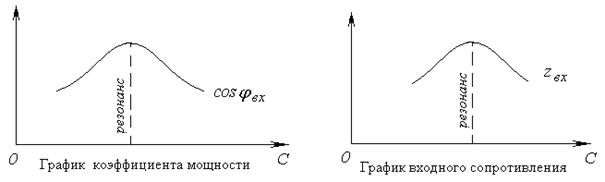
Рис. 5-5. Графики функциональных зависимостей в параллельной цепи

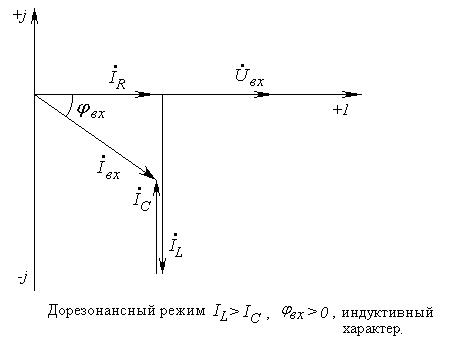
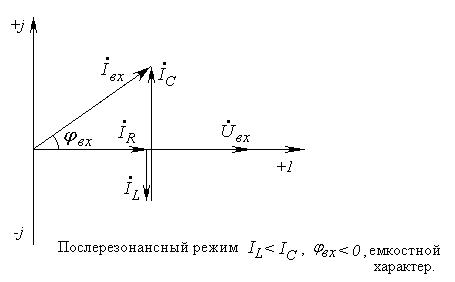
Рис. 5-6. Векторные диаграммы параллельной цепи для нерезонансных режимов

Для схемы (рис. 5-1) на основании векторных диаграмм для нерезонансных режимов (рис. 5-6) можно построить треугольник токов для всей цепи (рис. 5-7, a), а также для отдельной ветви в данном случае для ветви с катушкой (рис. 5-7. б). Для этой же ветви построен треугольник сопротивлений на рис. 5-7, в.

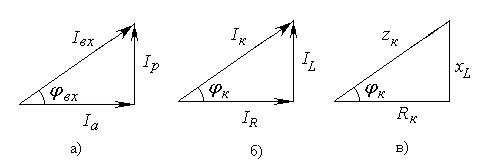
Рис. 5-7. Треугольники токов (а, б) и треугольник сопротивлений (в).

В схеме (рис. 5-1) активная составляющая входного тока, определяется активной составляющей тока катушки 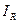.Если сопротивление ветви с катушкой не изменяется, то 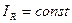, а следовательно, и .

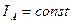Из треугольников рис. 5-7 следует:

cos φ_вх = I_a/I_вх; (5.7)

I_R = I_k cos φ_k; cos φ_k = R/Z_k

Следовательно,

(5.8)