Равносильность формул
Различные формулы могут иметь одинаковые таблицы истинности. Так возникает понятие равносильности формул.
Две формулы алгебры высказываний F1 и F2 называются равносильными (эквивалентными), если их таблицы истинности совпадают. Равносильность формул будем обозначать через F1≡F2. Нужно различать символы ↔ и ≡. Символ ↔ является символом формального языка, с помощью которого строятся формулы; символ ≡ заменяет слово «равносильно». Заметим, что отношение равносильности есть отношение эквивалентности. При этом справедливы утверждения:
1. Если две ПФ равносильны и одна из них содержит переменные, которых нет в другой, то ПФ от этих переменных не зависит (такие переменные называются фиктивными).
2. Если две ПФ равносильны, то их отрицания также равносильны.
3. Если в двух равносильных ПФ все вхождения некоторой переменной заменить любой формулой, то полученные новые ПФ будут равносильны.
Для любых формул X, Y, Z справедливы следующие равносильности (законы алгебры высказываний):
1. 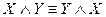 ,
, 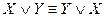 (коммутативность);
(коммутативность);
2. 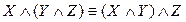 ,
, 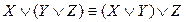 (ассоциативность);
(ассоциативность);
3. 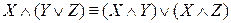 ,
, 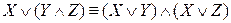 (дистрибутивность);
(дистрибутивность);
4. 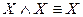 ,
, 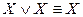 (идемпотентность);
(идемпотентность);
5. 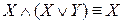 ,
, 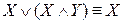 (законы поглощения);
(законы поглощения);
6. 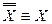 (закон двойного отрицания);
(закон двойного отрицания);
7. 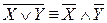 ,
, 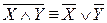 (законы де Моргана);
(законы де Моргана);
8. 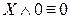 ,
, 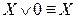 ,
, 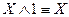 ,
, 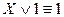 ,
, 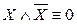 ,
, 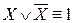 (законы, определяющие действия с константами);
(законы, определяющие действия с константами);
9. 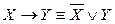 ,
, 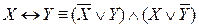 (исключение импликации и эквиваленции);
(исключение импликации и эквиваленции);
10. 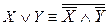 (исключение дизъюнкции);
(исключение дизъюнкции);
11. 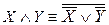 (исключение конъюнкции).
(исключение конъюнкции).
Любая равносильность может быть доказана либо с помощью таблиц истинности, либо равносильными преобразованиями. Докажем, например, равносильность для исключения импликации
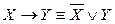 .
.
Для этого составим таблицы истинности для ПФ, стоящих в левой и правой частях выражения, и сравним их.
| Х | Y | 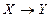
| 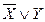
|
Пример.Доказать равносильность
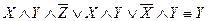
Используя закон поглощения, дистрибутивный закон и закон, определяющий действие с 1, получим
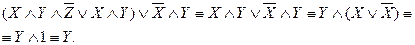
Понятия «равносильность» и «тавтология» связаны между собой следующим образом.
Теорема.F1≡F2 тогда и только тогда, когда F1↔F2 является тавтологией.
Справедливость этой теоремы вытекает непосредственно из определений ≡ и тавтологии.
Пример. Доказать 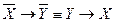 .
.
Покажем, что соответствующая эквиваленция является тавтологией.
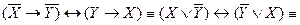
 |
Знание законов алгебры высказываний позволяет выполнять равносильные преобразования любых логических формул, сохраняя их значения для любых наборов пропозициональных переменных. Ниже на примерах рассмотрены равносильные преобразования основных логических операций.
Пример. X®Y º 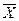 ÚY =
ÚY = 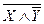 .
.
X«Y º(X®Y) Ù (Y®X) º ( 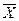 ÚY) Ù (
ÚY) Ù ( 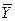 ÚX)
ÚX) 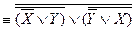 .
.
То есть операцию эквиваленции всегда можно заместить операций импликации и конъюнкции или дизъюнкции и отрицания.
Пример. X«Yº 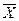 Ù
Ù 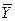 ÚXÙYº
ÚXÙYº 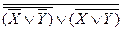 .
.
Выполненные примеры показывают, что всякую формулу алгебры логики можно заменить равносильной ей формулой, содержащей вместо импликации или эквиваленции только две логических операции: дизъюнкцию и отрицание или конъюнкцию и отрицание. Этот факт показывает, что множество логических связок дизъюнкции и отрицания, конъюнкции и отрицания формируют функционально полные алгебраические системы. Они достаточны для выражения любой логической функции
Если формула F содержит подформулу Fi, то замена подформулы Fi в формуле F на эквивалентную ей формулу Fj не изменяет значения формулы F при любом наборе пропозициональных переменных. Если необходима подстановка в формулу F вместо формулы Fi новой формулы Fj, то эту операцию нужно выполнить всюду по символу Fi .
Правила замены и подстановки расширяют возможности эквивалентных преобразований формул сложных высказываний.
Пример. Дано F=(X1®X2) ®((X2®X3) ®(X1ÚX2 ®X3)).
Выполним преобразования для упрощения алгебраического выражения.
1) Удалим всюду логическую связку ®:
F= 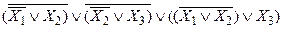 ;
;
2) Выполним преобразование по закону де Моргана:
F=X1Ù 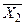 ÚX2Ù
ÚX2Ù 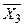 Ú
Ú 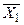 Ù
Ù 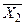 ÚX3;
ÚX3;
3) Выполним преобразование по закону дистрибутивности:
F=( X1Ú 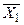 ) Ù
) Ù 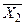 ÚX2 Ù
ÚX2 Ù 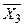 Ú X3;
Ú X3;
4) Удалить (X1Ú 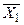 ), так как (X1Ú
), так как (X1Ú 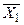 )=1:
)=1:
F= 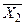 ÚX2Ù
ÚX2Ù 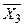 Ú X3;
Ú X3;
5) Выполним преобразование по закону дистрибутивности:
F= 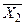 Ú(X2ÚX3) Ù (
Ú(X2ÚX3) Ù ( 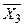 Ú X3);
Ú X3);
6) Удалим (X3Ú 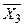 )=1:
)=1:
F= 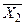 Ú(X2ÚX3);
Ú(X2ÚX3);
7) Применим закон ассоциативности:
F=( 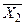 ÚX2)ÚX3;
ÚX2)ÚX3;
7) Удалим (X2Ú 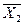 ), так как (X2Ú
), так как (X2Ú 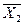 )=1:
)=1:
8) Получим
F=1ÚX3=1.
Пример. Дано рассуждение «или верно, что Петр поступил в университет (А), и при этом неверно, что Петр не поступил и Андрей не поступил, или Петр поступил и Семен поступил (С), или даже Петр поступил и Семен поступил, и Андрей поступил (В)».
Формула сложного высказывания имеет вид:
АÙ 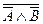 ÚАÙСÚАÙВÙС;
ÚАÙСÚАÙВÙС;
1) преобразуем формулу, используя закон де Моргана, получим:
АÙ(АÚВ)ÚАÙСÚАÙВÙС;
2) применим закон идемпотентности:
АÙ(АÚВ)ÚAÙАÙСÚАÙВÙС;
3) применить закон дистрибутивности по переменной А:
АÙ((АÚВ)ÚАÙСÚВÙС);
4) применим закон дистрибутивности по переменной С:
АÙ((АÚВ)Ú СÙ (АÚВ));
5) введем константу 1:
АÙ((АÚВ) Ù1Ú СÙ (АÚВ));
6) применить закон дистрибутивности для подформулы (АÚВ), получим:
АÙ(АÚВ) Ù (1ÚС);
7) удалим (1ÚС), получим:
АÙ (АÚВ);
8) применить закон поглощения, получим:
А.
Следовательно, в данном высказывании утверждается только то, что Петр поступил в университет, а об Андрее и Семене никакой информации нет.
Пример. Шесть школьников – Андрей, Борис, Григорий, Дмитрий, Евгений и Семен – участвовали в олимпиаде. Двое из них решили все задачи. На вопрос, кто решил все задачи, последовали ответы: 1) Андрей и Дмитрий; 2) Борис и Евгений; 3) Евгений и Андрей; 4) Борис и Григорий; 5) Семен и Андрей. В четырех из этих ответов одна часть неверна, другая верна. В одном – обе части неверны. Кто решил все задачи?
Введем обозначения:
A= «Андрей решил все задачи»;
Б= «Борис решил все задачи»;
Г= «Григорий решил все задачи»;
Д= «Дмитрий решил все задачи»;
Е= «Евгений решил все задачи»;
С= «Семен решил все задачи».
Так как в одном из ответов обе части неверны, а в остальных – одна, то необходимо составить пять формул, отражающих пять различных высказываний:
 Ù
Ù 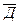 Ù (
Ù (  ÙЕÚБÙ
ÙЕÚБÙ  ) Ù (
) Ù (  ÙАÚЕÙ
ÙАÚЕÙ  ) Ù (
) Ù (  ÙГÚБÙ
ÙГÚБÙ 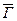 ) Ù
) Ù
Ù ( 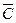 ÙАÚСÙ
ÙАÚСÙ  );
);
 Ù
Ù  Ù (
Ù (  ÙДÚАÙ
ÙДÚАÙ 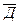 ) Ù (
) Ù (  ÙАÚЕÙ
ÙАÚЕÙ  ) Ù (
) Ù (  ÙГÚБÙ
ÙГÚБÙ 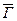 ) Ù
) Ù
Ù ( 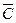 ÙАÚСÙ
ÙАÚСÙ  );
);
 Ù
Ù 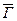 Ù (
Ù (  ÙДÚАÙ
ÙДÚАÙ 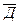 ) Ù (
) Ù (  ÙЕÚБÙ
ÙЕÚБÙ  ) Ù (
) Ù (  ÙГÚБÙ
ÙГÚБÙ 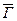 ) Ù
) Ù
Ù ( 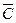 ÙАÚСÙ
ÙАÚСÙ  );
);
 Ù
Ù 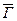 Ù (
Ù (  ÙДÚАÙ
ÙДÚАÙ 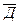 ) Ù (
) Ù (  ÙЕÚБÙ
ÙЕÚБÙ  ) Ù (
) Ù (  ÙАÚЕÙ
ÙАÚЕÙ  ) Ù
) Ù
Ù ( 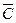 ÙАÚСÙ
ÙАÚСÙ  );
);
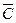 Ù
Ù  Ù (
Ù (  ÙДÚАÙ
ÙДÚАÙ 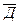 ) Ù (
) Ù (  ÙЕÚБÙ
ÙЕÚБÙ  ) Ù (
) Ù (  ÙАÚЕÙ
ÙАÚЕÙ  ) Ù
) Ù
Ù (  ÙГÚБÙ
ÙГÚБÙ 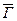 ).
).
Если допустить, что  º1 и
º1 и 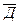 º1, то первая формула может быть записана так:
º1, то первая формула может быть записана так:
 Ù
Ù 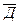 Ù (
Ù (  ÙЕÚБÙ
ÙЕÚБÙ  ) ÙЕÙ
) ÙЕÙ  Ù (
Ù (  ÙГÚБÙ
ÙГÚБÙ 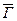 ) ÙСÙ
) ÙСÙ  ,
,
т. к. член  ÙАº0.
ÙАº0.
Если допустить, что  º1 и
º1 и  º1, то вторая формула может быть записана так:
º1, то вторая формула может быть записана так:
 Ù
Ù  Ù (
Ù (  ÙДÚАÙ
ÙДÚАÙ 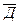 ) Ù
) Ù  ÙАÙ
ÙАÙ  ÙГÙ (
ÙГÙ ( 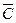 ÙАÚСÙ
ÙАÚСÙ  ),
),
т. к. члены ЕÙ  º0 и БÙ
º0 и БÙ 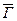 º0.
º0.
Если допустить, что  º1 и
º1 и  º1, то третья формула может быть записана так:
º1, то третья формула может быть записана так:
 Ù
Ù  Ù
Ù  ÙДÙБÙ
ÙДÙБÙ  Ù (
Ù (  ÙГÚБÙ
ÙГÚБÙ 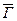 )ÙСÙ
)ÙСÙ  ,
,
т. к. члены АÙ 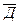 º0,
º0,  ÙЕ=0, и
ÙЕ=0, и 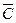 ÙАº0.
ÙАº0.
Если допустить, что  º1 и
º1 и 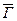 º1, то четвертая формула может быть записана так:
º1, то четвертая формула может быть записана так:
 Ù
Ù 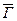 Ù(
Ù(  ÙДÚАÙ
ÙДÚАÙ 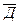 )Ù
)Ù  ÙЕÙ(
ÙЕÙ(  ÙАÚЕÙ
ÙАÚЕÙ  )Ù(
)Ù( 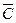 ÙАÚСÙ
ÙАÚСÙ  ), т. к. член БÙ
), т. к. член БÙ  º0.
º0.
Если допустить, что 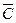 º1 и
º1 и  º1, то пятая формула может быть записана так:
º1, то пятая формула может быть записана так:
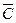 Ù
Ù  Ù
Ù  ÙДÙ (
ÙДÙ (  ÙЕÚБÙ
ÙЕÚБÙ  ) Ù ЕÙ
) Ù ЕÙ  Ù (
Ù (  ÙГÚБÙ
ÙГÚБÙ 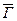 ),
),
т. к. член АÙ 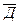 º0.
º0.
Применив законы дистрибутивности, идемпотентности и поглощения эти формулы можно упростить так:
 Ù
Ù 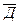 Ù
Ù  ÙЕÙГÙС;
ÙЕÙГÙС;
 Ù
Ù  Ù
Ù 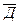 Ù
Ù 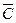 ÙАÙГ;
ÙАÙГ;
 Ù
Ù  Ù
Ù 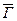 ÙДÙСÙБ;
ÙДÙСÙБ;
 Ù
Ù 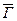 Ù
Ù  ÙДÙЕÙС;
ÙДÙЕÙС;
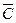 Ù
Ù  Ù
Ù  ÙДÙЕÙГ.
ÙДÙЕÙГ.
По условиям задачи только два участника решили все задачи. Поэтому формулы, содержащие по три пропозициональных переменных без отрицания, не отвечают поставленным условиям, а одна, содержащая только две переменных без отрицания, отвечает условиям задачи. Это формула  Ù
Ù  Ù
Ù 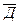 Ù
Ù 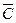 ÙАÙГ. Следовательно, все задачи на олимпиаде решили Андрей (А) и Григорий (Г).
ÙАÙГ. Следовательно, все задачи на олимпиаде решили Андрей (А) и Григорий (Г).
Дата добавления: 2015-04-10; просмотров: 1408;
