Таблицы истинности

Каждая пропозициональная переменная принимает значения 0 или 1, тогда ПФ в соответствии с определением логических операций также принимает значения 0 или 1, поэтому ее можно рассматривать как функцию, область значений и область определения которой совпадают и равны {0,1}. Такую функцию будем называть булевой функцией, двоичной или переключательной функцией.

Каждой ПФ, а значит и булевой функции, можно поставить в соответствие таблицу, называемую таблицей истинности, в которой перечислены все возможные значения входящих в нее переменных и значения ПФ или булевой функции на этих наборах. Каждый такой набор можно рассматривать как запись некоторого n-разрядного двоичного числа, при этом наибольшее двоичное число получим, составив набор из одних 1, а наименьшее – из одних 0. Таким образом, наибольшему числу соответствует десятичное число 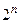– 1, а наименьшему – 0; всем остальным возможным наборам числа, заключенные между 0 и 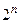–1. Это соответствие способствует упорядочению наборов аргументов булевой функции, которые заносятся в таблицу в порядке возрастания. Если функция зависит от n переменных, то таблица истинности содержит 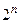наборов значений переменных.

С помощью таблицы истинности определяются все логические операции над высказываниями:

X	Y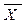

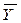
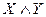
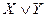
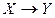
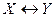
Пример. Рассуждение «если инвестиции на текущий год не из­менятся (A), то возрастет расходная часть бюджета (B) или возникнет безработица (C), а если возрастет рас­ходная часть бюджета, то налоги не будут снижены (D) и, наконец, если налоги не будут снижены и инвестиции не изменятся, то безработица не возникнет».

В этом рассуждении есть четыре повествовательных предложения, которые следует заменить пропозициональными переменными и формально описать суждение. Тогда формула сложного рассуждения имеет вид:

F =(A®(BÚC)) Ù (B®D) Ù ((DÙA)® ).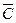

Для различных значений истинности пропозициональных переменных и подформул, построенных на логических операциях, можно последовательно определить значение истинности формулы F. Ниже представлена таблица истинности для этого рассуждения.

Для удобства записи любой подформулы и формулы каждый столбец пронумерован и логические операции выполняются с индексами столбцов.

Пример. Составим таблицу истинности для высказывания: «На экзамене я получу оценку «хорошо» или «отлично»». Выделим два простых высказывания: высказывание X= «На экзамене я получу оценку «хорошо»» и высказывание Y= «На экзамене я получу оценку «отлично»». Таблица истинности примет вид

По таблице истинности сложное высказывание «X или Y» можно представить как формулу 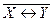, которую называют отрицанием эквивалентности или операцией сложения по модулю 2 и обозначают .

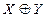ПФ называется тождественно истинной, общезначимой или тавтологией, если она принимает значение 1 на всех наборах значений переменных. Для обозначения того, что ПФ F есть тавтология используют запись ├ F.

ПФ называется тождественно ложной или противоречием, если она принимает значение 0 на всех наборах значений переменных.

ПФ называется выполнимой или опровержимой, если на некоторых наборах значений переменных она принимает значение 1, а на остальных – 0.

Тип ПФ можно определить с помощью таблицы истинности.

Пример. Определить тип ПФ 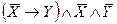. Для определения типа ПФ составим таблицу истинности

X	Y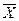

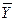
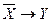
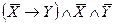
Как видно из таблицы истинности, данная ПФ является тождественно ложной, так как принимает значение 0 на всех наборах переменных.