Нормальные формы. Покажем, что для каждой ПФ существует ей равносильная специального вида
Покажем, что для каждой ПФ существует ей равносильная специального вида. Если Х – пропозициональная переменная, v есть 0 или 1, то выражение
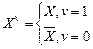
называется литерой. Литеры X и 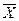 называются контрарными.
называются контрарными.
Заметим, что ПФ 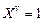 тогда и только тогда, когда
тогда и только тогда, когда 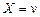 , то есть
, то есть 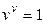 .
.
Следовательно, ПФ 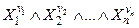 на наборе
на наборе 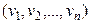 принимает значение 1, а на любом другом – значение 0. Аналогично ПФ
принимает значение 1, а на любом другом – значение 0. Аналогично ПФ 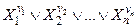 принимает значение 0 только на наборе (
принимает значение 0 только на наборе ( 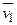 ,
, 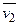 ,...,
,..., 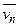 ), а на всех остальных наборах – 1 [3].
), а на всех остальных наборах – 1 [3].
 |
Теорема 5.5.1.Для любой ПФ имеет место равносильность
называемая дизъюнктивным разложением по переменной Х1.
Доказательство.
Пусть 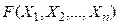 – произвольная ПФ. Определим значения левой и правой частей равносильности при Х1=1 и Х1=0.
– произвольная ПФ. Определим значения левой и правой частей равносильности при Х1=1 и Х1=0.
 |
При Х1=0 в левой части равносильности получаем ПФ
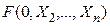 , а в правой части –
, а в правой части –
Таким образом, в левой и правой частях равносильности получаем одну и туже ПФ 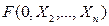 .
.
Аналогично можно показать, что при Х1=1 значением левой и правой частей равносильности является ПФ 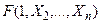 .
.
Итак, для любого набора значений переменных Х1, Х2, ..., Хn левая и правая части равносильности совпадают, что и доказывает справедливость теоремы.
Пример.Для ПФ 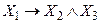 определить дизъюнктивное разложение по переменной Х1.
определить дизъюнктивное разложение по переменной Х1.
 |
Следствие.Для любой ПФ
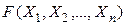 и любого натурального kимеет место равносильность
и любого натурального kимеет место равносильность
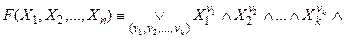
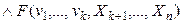 ,
,
называемая дизъюнктивным разложением 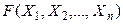 по переменным
по переменным 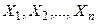 .
.
Теорема 5.5.2.Для любой ПФ имеет место равносильность
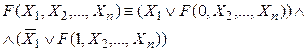
называемая конъюнктивным разложением по переменной Х1.
Доказательство теоремы 5.5.2 аналогично доказательству теоремы 5.5.1.
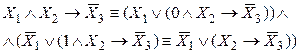
Пример.Для ПФ 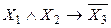 определить конъюнктивное разложение по переменной Х1.
определить конъюнктивное разложение по переменной Х1.
Следствие.Для любой ПФ 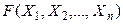 и любого натурального kимеет место равносильность
и любого натурального kимеет место равносильность
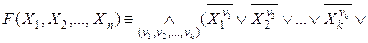
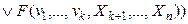 ,
,
называемая конъюнктивным разложением 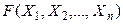 по переменным
по переменным 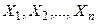 .
.
Таким образом, для любой ПФ существует равносильная ей, содержащая только константы 0 и 1, символы 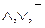 и переменные.
и переменные.
Определим некоторые канонические представления ПФ.
ПФ называется элементарной конъюнкцией (конъюнктом), если она является конъюнкцией переменных и отрицаний переменных (конъюнкцией литер).
ПФ называется элементарной дизъюнкцией (дизъюнктом), если она является дизъюнкцией переменных и отрицаний переменных (дизъюнкцией литер).
Пример.
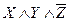 ,
, 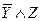 ,
, 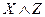 ,
, 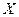 – элементарные конъюнкции.
– элементарные конъюнкции.
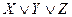 ,
, 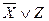 ,
, 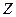 – элементарные дизъюнкции.
– элементарные дизъюнкции.
Говорят, что ПФ задана в дизъюнктивной нормальной форме (ДНФ), если она является дизъюнкцией элементарных конъюнкций.
Пример. 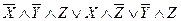 – ДНФ.
– ДНФ.
Говорят, что ПФ задана в конъюнктивной нормальной форме (КНФ), если она является конъюнкцией элементарных дизъюнкций.
Пример. 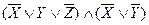 – КНФ.
– КНФ.
На основе равносильных преобразований любая формула может быть приведена к нормальной форме (ДНФ или КНФ) [3,4].
Алгоритм приведения ПФ к нормальным формам описывает следующая последовательность шагов.
1. Если ПФ содержит операции → и ↔, то их исключить с помощью равносильностей
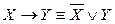 ,
, 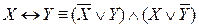 .
.
2. Привести отрицания к независимым переменным, используя законы де Моргана.
3. Раскрыть скобки по дистрибутивному закону конъюнкции относительно дизъюнкции для приведения к ДНФ или по дистрибутивному закону дизъюнкции относительно конъюнкции для приведения к КНФ.
Пример. Определить нормальные формы для ПФ 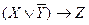 .
.
Действуя, в соответствии с алгоритмом, получим 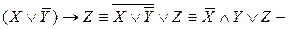 ДНФ.
ДНФ.
 |
Применяя к полученной ДНФ дистрибутивный закон дизъюнкции относительно конъюнкции, получим
Замечание. Для ПФ представление в виде нормальных форм не единственно. Переход от одной формы к другой осуществляется на основе равносильных преобразований.
В отличие от нормальных форм представление в виде совершенных нормальных форм является единственным.
Совершенной дизъюнктивной нормальной формой (СДНФ) данной ПФ называется ДНФ, в которой каждая элементарная конъюнкция содержит все переменные – без отрицания или с отрицанием, но не вместе.
Совершенной конъюнктивной нормальной формой (СКНФ) данной ПФ называется КНФ, в которой каждая элементарная дизъюнкция содержит все переменные – без отрицания или с отрицанием, но не вместе.
Существует два способа перехода к совершенным формам табличный и аналитический [2, 3, 4].
Дата добавления: 2015-04-10; просмотров: 1689;
