Табличный способ приведения к СКНФ

Используя таблицу истинности, можно составить СКНФ для ПФ. Для этого надо выполнить следующую последовательность шагов.

1. Составить таблицу истинности данной ПФ.

2. Рассмотреть те строки, в которых формула принимает истинностное значение 0. Каждой такой строке поставить в соответствие элементарную дизъюнкцию по правилу: переменная, принимающая значение 1, входит в нее с отрицанием, а 0 – без отрицания.

4. Образовать конъюнкцию всех полученных элементарных дизъюнкций, которая и составит СКНФ.

Пример.Привести ПФ 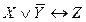к СКНФ. Построим таблицу истинности и на ее основе составим СКНФ.

X	Y	Z		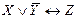Элементарные дизъюнкции

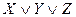
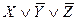
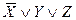
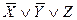
СКНФ примет вид

( ) ( ) ( ) ( ).

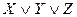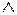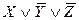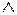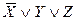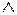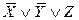Заметим, что из табличного способа построения совершенных нормальных форм следует, что тождественно ложные формулы не имеют СДНФ; тождественно истинные формулы не имеют СКНФ. Для выполнимых ПФ справедливы следующие теоремы:

Теорема 5.5.3.Если ПФ имеет СДНФ, то она единственна.

Теорема 5.5.4.Если ПФ имеет СКНФ, то она единственна.

Единственность совершенных нормальных форм у выполнимой ПФ обуславливает их использование для доказательства равносильностей, идея которого состоит в следующем: если у двух ПФ их СДНФ (СКНФ) совпадают, то они равносильны.

Пример.Доказать равносильность с помощью совершенных нормальных форм

.

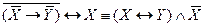Составим, например, СКНФ для ПФ, стоящих в левой и правой частях выражения.

:

:

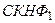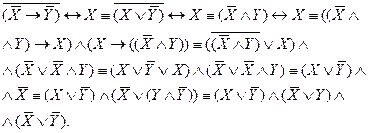
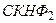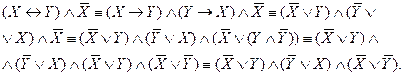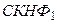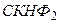Так как и совпадают, то исходные ПФ равносильны.

Пример. Доказать равносильность

.

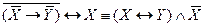Способ 1. Составим таблицы истинности для ПФ, стоящих в левой и правой части выражения и сравним их.

X	Y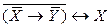

X	Y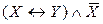

Как видим, таблицы истинности ПФ совпадают, следовательно, они равносильны.

Способ 2. Для доказательства равносильности двух ПФ составим новую формулу вида

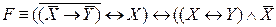
и докажем, что она является тавтологией. Для этого составим еe таблицу истинности

Способ 3. Чтобы доказать равносильность двух ПФ, приведем их к одной и той же более простой ПФ с помощью равносильных преобразований.

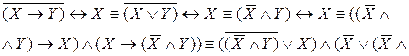
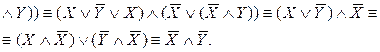
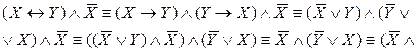
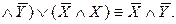
Таким образом,

.

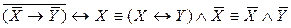5.6. Минимизация булевых функций в классе ДНФ

Всякую булеву функцию можно представить в ДНФ. Как известно, представление данной булевой функции в виде ДНФ можно осуществить не единственным образом. В связи с этим ставится вопрос о приведении булевой функции к такой ДНФ, которая была бы в некотором смысле наиболее простой по сравнению с другими ДНФ.

ДНФ называется минимальной, если она содержит по сравнению с другими эквивалентными ей формами минимальное количество символов (при подсчете символов учитывается каждое вхождение символа в формулу).

В простейших случаях минимизацию функции можно осуществить, выписав все ДНФ для этой функции и выбрав из них минимальную. Однако такой подход к решению задачи в общем случае может оказаться очень трудоемким. Поэтому рассмотрим другие способы решения задачи минимизации булевой функции в классе ДНФ.

Введем понятие импликанты булевой функции. Элементарную конъюнкцию 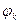назовем импликантой булевой функции f, если не существует такого двоичного набора переменных, при котором функция 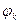принимает значение 1, а функции f – значение 0, т.е. .

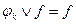Для того чтобы проверить является ли заданная элементарная конъюнкция импликантой функции f, следует всем переменным, входящим в эту конъюнкцию без отрицания, придать значение 1, а тем переменным, которые входят с отрицание – значение 0. При таких значениях переменных конъюнкция примет значение 1. Затем следует проверить, принимает ли функция f значение 1 при любых значениях остальных переменных.

Пример. Проверить, являются элементарные конъюнкци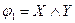и и 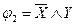импликантами булевой функции .

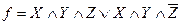Пологая в 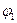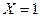, , 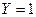получим

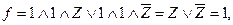
следовательно 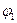– импликанта заданной булевой функции.

Пологая в 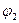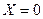, , 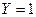получим

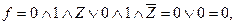
следовательно 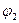не является импликантой заданной булевой функции.

Справедливы следующие теоремы:

Теорема 5.6.1. Если f₁, f₂,...,f_n – импликанты булевой функции f, то f₁Úf₂Ú...Úf_n и f₁Ù f₂Ù...Ùf_n также являются импликантами функции f.

Теорема 5.6.2. Если функция f₁Úf₂Ú...Úf_n есть импликанта функции f, то функции f₁, f₂,...,f_n также являются импликантами функции f.

Элементарная конъюнкция, входящая в ДНФ булевой функции f, называется ее простой импликантой, если никакая ее часть не является импликантной функции f.

Пример.

Простыми импликантами функции

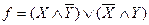являются функци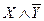и и .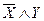

Теорема 5.6.3. Дизъюнкция всех простых импликант булевой функции равносильна этой функции.

ДНФ данной булевой функции, составленная из простых импликант, называется сокращенной ДНФ. Может случиться, что некоторые простые импликанты могут быть удалены и при этом значение функции не изменится ни на одном наборе. Такие простые импликанты называют лишними. Сокращенная ДНФ, из которой удалены все лишние импликанты, называется тупиковой ДНФ. Можно показать, что всякая тупиковая ДНФ является минимальной. Чтобы от сокращенной ДНФ перейти к минимальной, можно воспользоваться импликантной матрицей, в которой каждой строке соответствует простая импликанта, а каждому столбцу – конституента СДНФ данной булевой функции. Конституентой СДНФ называется элементарная конъюнкция, в которую входят все переменные. ДНФ, составленная из конституент, является СДНФ.

Импликантная матрица заполняется следующим образом: под конституентами, в которые входит данная простая импликанта, ставится «+», иначе «-». Каждая из конституент равна 1 лишь для одного набора аргументов. Для этого набора аргументов будут равны 1 те простые импликанты, которые расположены в строках, отмеченных «+». Поэтому достаточно оставить такие простые импликанты, чтобы в каждом столбце был хотя бы один «+».

Одним из наиболее распространенных методов минимизации является метод Квайна. В этом методе для приведения булевой функции к сокращенной ДНФ используются две специальные операции, основанные на свойствах булевых функций функций:

склеиванием по переменной Х в СДНФ называется равносильное преобразование типа

(X ÙF)Ú( 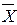ÙF)ºF;

поглощением в СДНФ называется равносильное преобразование типа

(FÙX)ÚFºF.

Правила склеивания и поглощения легко доказать с помощью таблиц истинности. Кроме этих правил, при минимизации булевых функций в классе ДНФ могут быть использованы любые известные равносильности.

Следующая последовательность шагов описывает метод Квайна минимизации булевой функции.

Шаг 1. Привести булеву функцию к СДНФ.

Шаг 2. В СДНФ произвести все возможные склеивания, а затем поглощения. Полученная на этом шаге ДНФ является сокращенной – она состоит из минимальных по числу множителей конъюнкций, но среди конъюнкций могут оказаться лишние.

Шаг 3. Перейти от сокращенной ДНФ к минимальной, используя импликантную матрицу.

Пример. Определить МДФ для булевой функции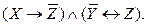

Решение. Для определения МДФ булевой функции воспользуемся методом Квайна. Приведем булеву функцию к СДНФ:

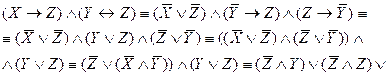
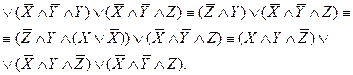
Перейдем от СДНФ к ДНФ, используя операции склеивания и поглощения:

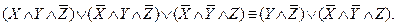
Построим импликантную таблицу

	+	+	-
	-	-	+

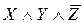
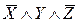
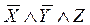
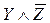
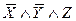
Достаточно оставить такие простые импликанты, чтобы в каждом столбце был хотя бы один “+”. Как видно, ни одно из слагаемых сокращенной формы исключить нельзя, поэтому МДФ имеет вид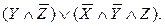

Замечание. Минимизированная форма для булевой функции может быть не единственна. При этом количество символов в различных минимизированных формах должно быть одинаковым.

Пример. Минимизировать булеву функцию f(0,1,1)=f(1,0,0)=f(1,0,1)=0 методом Квайна.

Булева функция задана перечислением наборов, на которых она принимает значение 0. На остальных наборах она принимает значение 1.

1. Составим таблицу истинности для приведения булевой функции к СДНФ.

x	y	z	f(x,y,z)	Элементарные конъюнкции

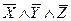
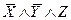
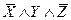
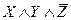
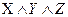
СДНФ примет вид

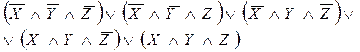
2. Произведем с СДНФ все возможные склеивания, а затем и поглощения:

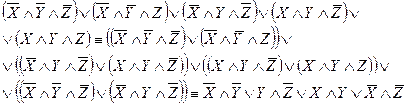
Получили сокращенную СДНФ:

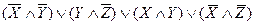
3. Перейдем от сокращенной СДНФ к минимальной, используя импликантную матрицу:

	+	+	-	-	-
	-	-	+	+	-
	-	-	-	+	+
	+	-	+	-	-

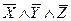
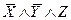
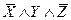
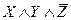
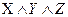
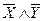
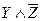
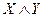
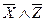
Достаточно оставить такие простые импликанты, чтобы в каждом столбце был хотя бы один «+», поэтому вторую или четвертую строку в импликантной матрице можно отбросить. Данная булева функция имеет две различные минимизированные формы

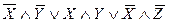и .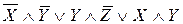

Задача минимизации булевых функций является важной для технических приложений логических функций и ей посвящено много работ, в которых предложены различные алгоритмы решения этой задачи.